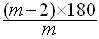محبوبترینها
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
پروازهای مشهد به دبی چه زمانی ارزان می‌شوند؟
تجربه غذاهای فرانسوی در قلب پاریس بهترین رستوران‌ها و کافه‌ها
دلایل زنگ زدن فلزات و روش های جلوگیری از آن
خرید بلیط چارتر هواپیمایی ماهان _ ماهان گشت
سیگنال در ترید چیست؟ بررسی انواع سیگنال در ترید
بهترین هدیه تولد برای متولدین زمستان: هدیه‌های کاربردی برای روزهای سرد
در خرید پارچه برزنتی به چه نکاتی باید توجه کنیم؟
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1830581961
چند وجهی های منظم - بخش سوم
واضح آرشیو وب فارسی:تبیان: چند وجهی های منظم - بخش سوم
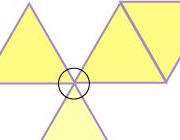
با نمایش کنج های یک مکعب توضیح دهید که برای ساختن یک چندوجهی باید در هر کنج تعدادی، حداقل سه عدد، چندضلعی منتظم مشابه را به هم بچسبانیم و تحقیق کنید آیا این کار را با هر چندضلعی می‌توان انجام داد؟ می دانیم که اگر از یک نقطه در صفحه تعدادی نیم خط خارج شود، مجموع زوایایی که این نیم خط ها با هم می سازند،360 درجه خواهد بود.
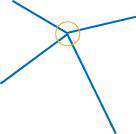
حال اگر چند زاویه در یک کنج چند ضلعی به هم رسیده باشند، در مورد مجموع آن ها چه می‌توان گفت؟ با باز کردن یک کنج، مثلاً از یک هرم، می‌توان پاسخ را یافت. بدون شک مجموع زوایای تشکیل دهنده یک کنج کم تر از 360 درجه خواهد بود.
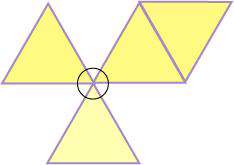
پس"چندضلعی‌های منتظم مشابه" فقط در صورتی یک کنج تشکیل می‌دهند که مجموع زوایای تشکیل دهنده ی کنج کم تر از ۳۶۰ درجه باشد. یعنی زاویه چندضلعی کم تر از ۱۲۰ درجه باشد ( حداقل سه چندضلعی داریم ). بنابراین اگر بدانیم اندازه ی زاویه‌های یکm-ضلعی منتظم چند درجه است، پاسخ سؤال اولیه هم روشن خواهد شد. دانش آموزان باید فرمول اندازه زاویه هایm-ضلعی منتظم را از کتاب های درسی به خاطر داشته باشند. اما بهتر است از آن‌ها بخواهید که این فرمول را محاسبه کنند:
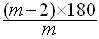
روی تخته محاسبه کنید. ۳ ضلعی منتظم (۶0) درجه، ۴ ضلعی منتظم ( ۹۰ درجه)، ۵ ضلعی منتظم ... ۶ ضلعی منتظم ( ۱۲۰ درجه )... ۷ ضلعی منتظم ... بنابراین فقط با ۳ ضلعی، ۴ ضلعی و ۵ ضلعی منتظم می‌توان چندوجهی منتظم ساخت. حال از دانش اموزآن بخواهید تمام کنج های ممکن را لیست کنند. برای این کار می‌توانید تعدادی چند ضلعی منتظم کاغذی و مقداری چسب در اختیار آن‌ها قرار دهید تا بتوانند کنج‌ها را به طور عملی بسازند و همین طور مشاهده کنند که ساختن بعضی از کنج‌ها ممکن نیست. لیست ساخته شده در پایان کار باید به شکل زیر باشد. کنج ساخته شده از ۳ تا ۳-ضلعی منتظم ( مجموع زوایا ۱۸۰ درجه ) کنج ساخته شده از ۴ تا ۳-ضلعی منتظم ( مجموع زوایا ۱۸۰ درجه ) کنج ساخته شده از ۵ تا ۳-ضلعی منتظم ( مجموع زوایا ۱۸۰ درجه ) کنج ساخته شده از ۳ تا ۴-ضلعی منتظم ( مجموع زوایا ۱۸۰ درجه ) کنج ساخته شده از ۳ تا ۵-ضلعی منتظم ( مجموع زوایا ۱۸۰ درجه ) بعد از تکمیل لیست از آن ها بپرسید هر کدام از این کنج‌ها متعلق به کدام چند وجهی است. مثلاً به راحتی می‌توان حدس زد که مورد دوم، متعلق به یک مکعب است. اما بقیه ی موارد چه طور؟ از دانش آموزان بخواهید سعی کنند تا آن جا که امکان دارد تصوری از این چندوجهی‌ها در ذهن خود داشته باشند و آن را توصیف کنند. ممکن است در این جا با معرفی چندوجهی های منتظم به دانش آموزان با استفاده از تصویر یا ماکت و نشان دادن این که این چندوجهی‌ها کنج هایی با مشخصات بالا دارند، به کلاس خاتمه دهید و یا به سراغ بخش ساخت چندوجهی بروید. اما اگر فرصت بیش تری دارید و دانش آموزان علاقه مند هستند، می‌توانید بحث را با بخش بعد ادامه دهید. در بخش بعد مشخصات این چندوجهی‌ها را به طور دقیق توضیح خواهیم داد و تعداد رأس ها، ضلع‌ها و وجه های هرکدام را محاسبه خواهیم کرد. دیدن چندوجهی‌ها بعد از این مرحله می‌تواند جذاب تر باشد. بخش اول بخش دوم بخش چهارم صفحه اصلی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 4372]
-
گوناگون
پربازدیدترینها