محبوبترینها
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1847235100
چند وجهی های منتظم - بخش دوم
واضح آرشیو وب فارسی:تبیان: چند وجهی های منتظم - بخش دوم در بخش اول هدف این است که دانش آموزان با مشاهده ی اجسام و تصاویر روی کاغذ و تخته و با بحث کردن با هم با راهنمایی معلم، مفهوم منتظم بودن چندضلعی و نیز چندوجهی را درک کنند. تعدادی تصویر چند ضلعی در اختیار دانش آموزان قرار دهید ( بهتر است قبل از شروع کلاس تخته را با تصاویر چند ضلعی‌ها پر کرده باشید ).
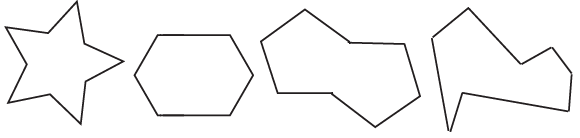
از دانش آموزان بپرسید کدام یک از چند ضلعی‌ها منتظم هستند. با سؤال کردن در مورد تک تک تصویرها و دانستن نظر دانش آموزان در مورد منتظم و یا نا منتظم بودن آن ها تعریف دقیقی از چند ضلعی منتظم ارائه دهید. مثلاً چند ضلعی اول به نظر هیچ کس منتظم نمی آید چون هیچ نظمی درآن به چشم نمی خورد. در چند ضلعی دوم، طول اضلاع مساوی است اما باز هم چندان منتظم به نظر نمی رسد، چرا که زاویه های آن مساوی نیست. بنابراین با استفاده از این شکل میتوان نشان داد که برای منتظم بودن، مساوی بودن طول اضلاع کافی نیست. چند ضلعی سوم زاویه های برابر دارد اما طول اضلاع آن با هم مساوی نیست و ... در ابتدا با مطرح کردن سؤالاتی که پاسخ دادن به آن‌ها برای بیش تر دانش آموزان ممکن است آن ها را وارد بحث و به آن علاقه‌مند کنید. با طرح هر سؤال زمانی را به دانش آموزان فرصت دهید. اگر دو معلم در کلاس حضور داشته باشند یکی از آن‌ها می‌تواند با مطرح کردن پرسش‌ها در کنار تخته جریان کلی کلاس را اداره کند، و دیگری می‌تواند با دانش آموزان صحبت کند و آن‌ها را درگیر بحث و در صورت لزوم راهنمایی کند. حال باید معادل‌های سه بعدی چندضلعی‌ها یعنی چندوجهی‌ها را معرفی کنید. این کار را می‌توانید با تعدادی تصویر و یا چند وجهی ساخته شده انجام دهید. یک چند ضلعی از چند نقطه به عنوانرأس و چند پاره خط به عنوان ضلع تشکیل شده است. یک چندوجهی نیز از چند نقطه به عنوان رأس، چند پاره خط به عنوان ضلع یا یال و چند صفحه به عنوان وجه تشکیل شده است. این توصیف ساختاری نشان می‌دهد که چندوجهی‌ها به گونه ای معادل های سه بعدی چندضلعی‌ها هستند.
به دانش آموزان کمک کنید تا با تعمیم تعریف چند ضلعی منتظم تعریفی از چندوجهی منتظم ارائه دهند. همان طور که منتظم بودن یک چندضلعی مستلزم برابر بودن عناصر سازنده ی آن یعنی زاویه‌ها و ضلع‌ها است، عناصر تشکیل دهنده یک چندوجهی منتظم نیز باید با هم برابر باشند. تعریف هایی را که دانش اموزان مطرح می‌کنند روی تخته لیست کنید و با کمک آن‌ها، اطلاعات را دسته بندی و ساده کنید تا به این تعاریف برسید: هر وجه، یک چندضلعی منتظم می باشد. همه ی وجه‌ها با هم برابر می باشند. در هر رأس تعداد مساوی از وجه‌ها یا یال‌ها به هم برسند. ممکن است تعریف هایی که مطرح می‌شوند از این قرار باشند: همه ی ضلع‌ها با هم برابر باشند، همه ی زاویه های روی وجه‌ها با هم برابر باشند. همه ی کنج‌ها به یک شکل باشند. توجه کنید که از جمله ی اول و دوم میتوان شرط دوم تعریف را نتیجه گرفت و جمله ی سوم به نوعی برابر با شرط های دوم و سوم است. بنابراین شکل بیان تعریف از سوی دانش اموزان چندان مهم نیست، مهم آن است که این مفهوم را درک کنند و بفهمند که یک مفهوم واحد می‌تواند بیان های متفاوتی داشته باشد. از دانش آموزان سؤال کنید که آیا می توانند تعداد چند ضلعی های منتظم را حدس بزنند؟ احتمالاً به راحتی پاسخ خواهند داد برای هر عدد طبیعی n ، یک n-ضلعی منتظم وجود دارد. سؤال دیگری که میتوان مطرح کرد این است که چه تعداد چندوجهی منتظم وجود دارد؟ در بخش بعد نشان خواهیم داد برخلاف انتظار فقط تعداد کمی چند وجهی منتظم وجود دارد.
بخش اول بخش سوم بخش چهارم صفحه اصلی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 7376]
-
گوناگون
پربازدیدترینها