محبوبترینها
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
پروازهای مشهد به دبی چه زمانی ارزان می‌شوند؟
تجربه غذاهای فرانسوی در قلب پاریس بهترین رستوران‌ها و کافه‌ها
دلایل زنگ زدن فلزات و روش های جلوگیری از آن
خرید بلیط چارتر هواپیمایی ماهان _ ماهان گشت
سیگنال در ترید چیست؟ بررسی انواع سیگنال در ترید
بهترین هدیه تولد برای متولدین زمستان: هدیه‌های کاربردی برای روزهای سرد
در خرید پارچه برزنتی به چه نکاتی باید توجه کنیم؟
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1827741744
ارائه اعداد
واضح آرشیو وب فارسی:تبیان: ارائه اعداد
توضیح اولیهسؤالاتی برای دانش آموزانبرای تبدیل عدد n از مبنای 10 به مبنای b، نامعادله ای بنویسید که شامل n و b و p باشد، p بزرگترین توان b است که برای ساختن عدد n لازم است. برای پیدا کردن b چه باید کرد؟نامعادله ی bp < n < bp + 1 را بنویسید، با حل این نامعادله بزرگ ترین p را خواهید یافت.اگر بخواهیم از الگوریتم تقسیم های متوالی استفاده کنیم، چرا باقی مانده از مقسوم علیه بیشتر نمی شود؟ اگر باقی مانده بزرگتر از مقسوم علیه باشد، به این معناست که خارج قسمت درست نبوده و گروه های بیشتری از سایز d را می توان از مقسوم برداشت. تقسیم مکرر چه امتیازی بر تفریق مکرر برای تبدیل یک عدد به مبنای دیگر دارد؟تقسیم های مکرر از نظر محاسبه موثرترند.چرا ارائه ی فیبوناچی هیچ وقت شامل دو عدد یکسان متوالی نمی شود؟طبیعت الگوی فیبوناچی این است که هر عدد مساوی حاصل جمع دو عدد قبلی است.در نتیجه هر دو یک یکسان متوالی باید با صفر جایگزین شود و ارزش مکانی بزرگتر بعدی باید یکی بیشتر شود. مثلاً ارائه نادرست فیبوناچی 110 می تواند به عنوان حاصل جمع دستی مال 5=0+2+5+3 تفسیر شود؛ اما از آن جا که 5 یک عدد فیبوناچی است، این را می توان در عوض به عنوان 1000 معرفی کرد. فعالیت های اضافی1- جدول هایی برای جمع و ضرب مبنای 6 درست کنید.2- 2006 را از مبنای 10 به مبنای 6 تبدیل کنید . اشاره : به اعداد فرد توجه کنید. عکس العمل معلم1- چرا باید دانش آموزان تمرین کنند که اعداد را به عنوان حاصل جمع مضارب توان های 10 تفسیر کنند؟2- آیا تمرین های این درس برای دانش آموزان سخت بود؟ چطور می توانید تمرین ها را برای دانش آموزان ضعیف تر ، آسان تر کنید یا برای دانش آموزان زرنگ تر، سخت تر کنید؟3- آیا در ضمن تدریس به تجربیات جدیدی رسیده اید، چگونه می تون از این تجربیات استفاده کرد؟ اهداف- مبنای ارائه ی یک عدد صحیح در مبنای b را پیدا کنید.- عددی را با مبنای b توضیح دهید. وسایل لازم- برگه ی فعالیت مبنای دودویی- برگه ی فعالیت ارزش مکانی طرح درسدر کلاس های پایین تر، دانش آموزان یاد می گیرند که یک عدد طبیعی در مبنای 10 حاصل جمع مضرب های مختلفی از توان های طبیعی 10 است. در این درس از دانش آموزان خواسته می شود یک عدد فرضی در مبنایی به جز 10 را به صورت حاصل جمع مضرب هایی در مبنای b توضیح دهند. سرانجام دانش آموزان دو روش را برای نوشتن یک عدد صحیح فرضی در مبنای b یاد می گیرند.با یادآوری ارزش مکانی شروع کنید و یک مثال بزنید مثلاً توضیح ارزش مکانی 4273 چنین می شود 3+70+200+4000 .توجه کنید که 4000=4(10)3 مضربی از توان سه عدد 10 است. به همین ترتیب ، 3(10)0 ،7(10)1 ،2(10)2 مضرب های از توان های مختلف 10 هستند. شکل زیر را مشاهده کنید:
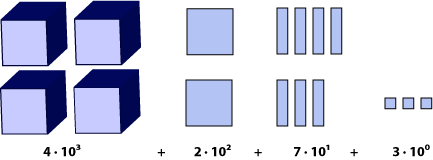
دیاگراموقتی عددی به جای مبنای 10 در مبنای b بیان می شود، باز هم این چنین توضیح داده می شود. فرض کنید b=6 . مراحلی که در پایین نشان داده شده، کاربردی است و اهمیتی ندارد عدد b چقدر است. عدد 6(2113) به صورت حاصل جمع مضارب توان های مختلف 6 تفسیر می شود. همان طور که 4273 به صورت حاصل جمع مضارب توان های 10 در بالا تفسیر می شد. اگر عددی در مبنای 10 نوشته شود، نوشتن مبنا ضروری نیست اما نوشتن مبناهای غیر 10 الزامی است. به عنوان مثال: (2113)6 = 2(63) + 1(62) + 1(61) + 3(60) = 477 داریم. به این ترتیب 21136 به عنوان 477 تفسیر می شود. عملیات معکوس این روش هم به عملیاتی است که عدد در مبنای 6 را به عددی در مبنای 10 می برد.دانش آموزان را طی مراحل تفریق ها و تقسیم های مکرر برای تبدیل عدد در مبنای ده 477 به مبنای 6 راهنمایی کنید. تفریق مکرربرای نوشتن عدد 477 در مبنای 6 ابتدا تمام توان های طبیعی عدد 6 که کمتر از 477 است را تعیین کنید. 60 = 1, 61 = 6, 62 = 36, 63 = 216(توجه کنید که توان بعدی 6 یعنی 64 بزرگتر از 477 است.)در گام بعدی، همان طور که معلوم است 477 را از بزرگترین توان 6 کم می کنیم. با انجام اولین تفریق، میزان باقی مانده 261=216-477 خواهد بود. در این مرحله، عددمان 261 است زیرا هنوز باقی مانده بزرگتر از 216=63 است، بنابراین 45=(216)2-477 پس عددمان می شود 45. حالا چون عددمان از 216=63 کوچکتر است اما بزرگتر از 216=62 است، باز هم 36 را تفریق کنید. می شود 9=36-45اگر همه این ها را کنار هم بگذاریم می شود 9+(36)1+(216)2=477 به عنوان حاصل جمع مضارب توان های 6 عدد باقی مانده 9 است. (1)3+(6)1=9تمام این عملیات عدد 477 را می دهد 477 = 2(63) + 1(62) + 1(61) + 3(60) = 21136 این نتیجه با نتیجه قبلی مطابقت می کند. در این مرحله از هر دانش آموز بخواهید اعداد سه رقمی دلخواهی را انتخاب کنند و با استفاده از روش فوق آن اعداد را در مبنای 6 بنویسند. برای افزایش مهارت در این کار، از آن ها بخواهید که اعدادی را که به مبنای 6 برده اند، در اختیار دوستان خود قرار دهند تا آن ها در فرایندی برعکس، عدد را در مبنای 10 برده و با عدد اولیه مقایسه کنند. تفریق های مکرر نسبت به تقسیم های مکرر دو امتیاز دارد اول این که این روش به تعریف ارتباط دارد، بنابراین به درک بهتری منجر می شود. دوم این که می توان در موقعیت هایی که نمی توان از تقسیم استفاده کرد، از آن استفاده کرد. مثل مسئله fibonancci که در پایین توضیح می دهیم. تقسیم های مکررمراحل تقسیم مکرر به تقسیم دائمی بر مبنای b و تفسیر نتایج نیاز دارد.وقتی بخواهیم عدد 4237 را در مبنای 10 بنویسیم؛ عدد را بر 10 تقسیم می کنیم باقی مانده 7 و خارج قسمت 423 می شود. در مرحله ی بعد 423 را بر 10 تقسیم کرده، مقدار باقی مانده 7 است که رقم tens 4273 است. با استفاده از الگوریتم فوق هم می توان اعداد را به مبناهای مختلف b برد. اگر b منفی باشد، باز هم این الگوریتم صحیح است. با استفاده از الگوریتم تقسیم های مکرر برای نوشتن 477 در مبنای 6، اول 477 را تقسیم بر 6 کنید. این تقسیم خارج قسمت 79 و باقی مانده 3 را به شما می دهد. به بیان دیگر 3+(79)6=477 (توجه داشته باشید که باقی مانده هیچ وقت از 5 بزرگتر نیست چون در این صورت خارج قسمت بزرگتر بوده سپس خارج قسمت را تقسیم بر 6 کنید و خارج قسمت و باقی مانده جدید را یادداشت کنید. به این ترتیب 1+(13)6=79 عملیات را تکرار کنید: 1+(2)6=13 و سرانجام 2+(0)6=2 . نوشتن باقی مانده ها به صورت معکوس عدد 2113 را در مبنای 6 می دهد.برای تصویر کردن بیشتر این مرحله ، این مثال را بررسی کنید. برای این که بفهمید چرا 21136=477 می شود، بارها و بارها هر یک از خارج قسمت ها را با ارزشی که در طول مرحله تقسیم به دست آمده، جایگزین کنید. در نتیجه : 477 = 6(79) + 3 = 6(6(13)+1) + 3 = 6(6(6(2) + 1) + 1) + 3 = 6(6)(6)(2) + 6(6)(1) + 6(1) + 3 = 2(63) + 1(62) + 1(61) + 3(60) = 21136 امتیاز تقسیم های مکرر بر تفریق های مکرر این است که روش اول از نظر محاسبه، موثر ترند. همچنین روش توجیه آن هم می تواند در موقعیت های دیگر به کار رود. در این مرحله از دانش آموزان بخواهید یک عدد سه رقمی انتخاب کنند و با روش تقسیم های مکرر آن را در مبنای 6 بنویسند. سرانجام باید عددشان را در فرایندی معکوس در مبنای 10 بنویسند. یک راهکار دیگر می تواند این باشد که دانش آموزان در گروه های دوتایی کار کنند تا اعداد در مبنای 6 را پیدا کنند. وقتی ارائه کامل شد، می توانند جواب هایشان را با گروه های دیگر مبادله کنند. از دانش آموزان بخواهید برگه ی فعالیت مبنای دودویی را کامل کنند.
مبنای دودوییاین صفحه شامل نوشتن اعداد 0 تا 31 در مبنای 2 است و می توان به تنهایی آن را کامل کرد، اگر چه کارکردن دانش آموزان به طور گروهی، خطاها را کاهش می دهد و زمان لازم برای تکمیل کردن آن هم کمتر می شود. از دانش آموزان بخواهید سمت راست و چپ صفحه را برای یافتن شباهت ها مقایسه کنند. الگوی صفرها و یک ها را در هر ستون در نظر بگیرید. دانش آموزان ممکن است متوجه این موارد شوند: - در ستون سمت راست 1 صفرها و یک ها متغیرند.- در ستون بعدی 2 الگوی دو صفر، دو یک، دو صفر ، دو یک وجود دارد.- در ستون بعدی 4 الگوی چهار صفر، چهار یک ، چهار صفر، چهار یک وجود دارد.- در ستون بعدی 8، الگوی هشت صفر، هشت یک ، هشت صفر ، هشت یک هست.- ستون منتها الیه چپ 16، شامل صفرهایی در طول سمت چپ جدول و یک هایی درسمت راست جدول است. در این مرحله دانش آموزان باید بتوانند سوالات 4-1 برگه ی فعالیت ارزش مکانی را حل کنند. سؤالات مشکل تر هم در آخر صفحه فعالیت وجود دارد.
ارزش مکانیتوجه کنید: قبل از شروع درس، شاید بخواهید راه حل ها را بررسی کنید. ارائه فیبوناچیمثل هر عدد مثبتی که می تواند به عنوان حاصل جمع توان های مشخص 2 و 6 یا 10 بیان شود، هر عددی را می توان به عنوان حاصل جمع اعداد فیبوناچی نشان داد.این کار را با چند راه می توان انجام داد اما روشی که در این درس ارائه می شود، الگوریتم طماع است. اسمش طماع است زیرا در هر مرحله، بزرگترین عدد ممکن انتخاب می شود.این روش بر مبنای تفریق های مکرر است. برای نشان دادن عدد N، بزرگترین عدد فیبوناچی را انتخاب کنید، عددی که از N بزرگتر نباشد، بعد آن را تفریق کنید و با اختلاف باقی مانده هم این کار را ادامه دهید. مثلا فرض کنید N=100 بزرگترین عدد فیبوناچی کوچکتر از 100، 89 است بنابراین 89 را تفریق کنید. حاصلش می شود 11=89-100. حالا که 11 کوچکتر از اعداد فیبوناچی 55 و 34 و 21 و 13 است نمی شود آن را تفریق کرد. عدد فیبوناچی بعدی که می توان تفریق کرد 8 است و 3=8-11 . چون 3 یک عدد فیبوناچی است پس تفریق تکمیل شده است.برای تفسیر نتایج، اعداد اصلی را به عنوان حاصل جمع اعداد فیبوناچی بنویسید. 100 = 1(89) + 0(55) + 0(34) + 0(21) + 0(13) + 1(8) + 0(5) + 1(3) + 0(2) + 0(1) = 1000010100f این تمرین را با دانش آموزانتان انجام دهید و از آن ها بخواهید تبدیل ها را انجام دهند. مطمئن شوید عددی را که در ابتدا گفتید به دست می آورند.به علاوه محاسبه در مبنای فیبوناچی چیزی است که سرانجام تمام دانش آموزان باید بتوانند انجام دهند. 10000 و 1010 و 1001 و 1000 و 101 و 100 و 10 و 1 (توجه کنید که محاسبه به اعداد فیبوناچی سوال ماقبل آخر برگه فعالیت است.) دانش آموزان همچنین باید بتوانند فکر کنند که چرا ارائه های فیبوناچی هرگز دو یتا یک متوالی وجود ندارد و این به عددی که ارائه می شود، ندارد.در درس دیگر این بخش، مبنای فیبوناچی برای بازی متغیر "نیم" به کار رفته است. گزینه های ارزیابی1- سوالات 4-1 را در روز اول درس معین کنید. سؤالات 8-5 را می توان به عنوان تکلیف درسی، روز بعد از درس مطرح کرد.2- از دانش آموزان بخواهید الگوریتم تفریق های مکرر و تقسیم های مکرر را برای دوستشان توضیح دهند. سپس از هر دانش آموز بخواهید پاراگرافی در این مورد بنویسد که چرا این الگوریتم ها مؤثر است. مترجم: فاطمه وفاییتنظیم: نسرین صادقی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 4842]
-
گوناگون
پربازدیدترینها