پرچم تشریفات با کیفیت بالا و قیمت ارزان
پرواز از نگاه دکتر ماکان آریا پارسا
دکتر علی پرند فوق تخصص جراحی پلاستیک
تجهیزات و دستگاه های کلینیک زیبایی
سررسید تبلیغاتی 1404 چگونه میتواند برندینگ کسبوکارتان را تقویت کند؟
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارشهای سیلآسا در راه است! آیا خانه شما آماده است؟
بارشهای سیلآسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
تعداد کل بازدیدها :
1850705486

قانون سینوس ها
واضح آرشیو وب فارسی:تبیان: قانون سینوس هااهدافدانش آموزان بعد از این درس می توانند:با استفاده از مثلثات مثلث قائم الزاویه، قانون سینوس ها را بسط دهند. با استفاه از قانون سینوس ها، مسائل را حل کنند. وسایل لازمبرگه ی فعالیت قانون سینوس ها در این درس، دانش آموزان با استفاده از روابط مثلثاتی در مثلث قائم الزاویه، قانون سینوس ها را بسط می دهند. طرح درسشاید پیش از این، دانش آموزان از مثلثات، برای حل مسائل مثلث قائم الزاویه استفاده می کردند. در این درس، استفاده از مثلثات برای حل مسائل مثلث های غیر قائم الزاویه به دانش آموزان آموزش داده می شود. درس را با ترسیم مثلث ABC بر روی تخته سیاه یا پروژکتور آموزشی شروع کنید:
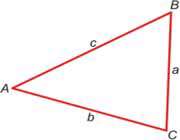
برای بحث دقیق تر، اعداد زیر را به شکل اضافه کنید:

پرسش های زیر را مطرح کنید: آیا تنها یک مثلث با زوایا و اضلاع داده شده، وجود دارد؟ چرا؟ [بله، دو زاویه و یک ضلع یکی از حالت های تساوی دو مثلث است. بنابراین، اگر دو زاویه و یک ضلع مثلث معلوم باشد، آن مثلث یکتا است.] چگونه می توان ضلع و زاویه ی سوم مثلث را پیدا کرد؟ (نیازی به ارائه ی عدد نیست، فکر کنید چگونه می توان روشی برای یافتنن ضلع و زاویه ی سوم پیدا کرد؟) [می دانیم مجموع زوایای داخلی هر مثلث، 180 درجه است. با توجه به این که دو زاویه ی مثلث، معلوم است آن ها را با هم جمع و از 180 درجه کم کنید تا زاویه ی سوم به دست بیاید. یافتن اندازه ی ضلع سوم، کمی مشکل تر است. هدف این درس، یافتن روشی برای تعیین ضلع سوم است.] از دانش آموزان بخواهید تا به صورت انفرادی به این پرسش فکر کنند. سپس از آن ها بخواهید تا نظراتشان را با اعضای گروه در میان بگذارند. از همه ی گروه ها بخواهید در این مورد بحث کنند. پس از بحث درباره ی این پرسش، برگه ی فعالیت قانون سینوس ها را بین دانش آموزان توزیع کنید و از آن ها بخواهید مقدمه ی آن را بخوانند.

برگه ی فعالیت قانون سینوس هاحالا میان مسئله ای که در ابتدای کلاس بیان شد و هدف این فعالیت ارتباط ایجاد کنید. برای دانش آموزان توضیح دهید که در این فعالیت، علاوه بر حل مسائل مثلث های قائم الزاویه، به دنبال روشی برای حل مسائل مربوط به مثلث های غیر قائم الزاویه هستیم. برگه ی فعالیت قانون سینوس هادر برگه ی فعالیت، دستور کارهایی ارائه شده که دانش آموزان را برای انجام فعالیت راهنمایی می کند. هنگامی که دانش آموزان فعالیت را انجام می دهند، معلم باید نقش های گوناگونی ایفا کند. در شش پرسش اول فعالیت، معلم باید فقط مطالب را توضیح دهد و نقش توضیح دهنده را دارد. قبل از این که دانش آموزان کار روی این فعالیت را شروع کنند، معلم باید موارد زیر را توضیح دهد: ارتفاع مثلث، خطی است که از یک ر?س مثلث خارج شده و بر ضلع مقابل آن ر?س، عمود می شود. با رسم یک ارتفاع در مثلث ABC، دو زاویه ی قائمه ایجاد می شود. با توجه به این که دو زاویه ی قائمه ایجاد شده، می توان از مثلثات مثلث قائم الزاویه ای که درست شد، برای توضیح روابط میان زاویه ها و اضلاع هر یک از مثلث ها استفاده کرد. با توجه به این که مثلث ABC یک ضلع و یک زاویه ی مشترک با هر یک از دو مثلث ایجاد شده دارد، می توان از روابط میان زوایا و اضلاع مثلث قائم الزاویه برای توضیح روابط میان زوایا و اضلاع مثلث ABC استفاده کرد. از دانش آموزان بخواهید تا درباره ی پرسش های 1 و 2 در برگه ی فعالیت فکر کنند. در مثلث ABC، ارتفاع ر?س B را رسم کنید. برای توضیح روابط در مثلث قائم الزاویه و مثلث ABC، از شکل استفاده کنید. دانش آموزان را راهنمایی کنید تا درباره ی پرسش 3 کار کنند و پاسخ های خود را با هم گروهی های خود بررسی کنند. پس از اتمام وقت، از آن ها بخواهید تا معادله هایی را که نوشته اند تحویل دهند. معادله ها را بر روی تخته یا پروژکتور بنویسید. به دانش آموزان توضیح دهید که در همه ی معادله ها، ارتفاع k ظاهر می شود. از آن ها بپرسید: "چرا ارتفاع k در همه ی معادله ها وجود دارد؟" [k ضلع مقابل به دو زاویه ی A و C در هر یک از مثلث های قائم الزاویه است.] دانش آموزان را هدایت کنید تا روی پرسش 4 کار کنند و در مورد پاسخ های خود با هم گروهی شان بحث کنند. پس از اتمام وقت، از آن ها بخواهید تا معادله هایی را که نوشته اند تحویل دهند. معادله ها را بر روی تخته سیاه یا پروژکتور بنویسید. سپس توضیح دهید چون هر دو رابطه در پرسش 4 مساوی k است، می توان آن ها را مساوی هم قرار داد. از دانش آموزان بپرسید چرا می توان آن دو رابطه را مساوی هم قرار داد؟ [به دلیل اصل تساوی که اگر دو چیز برابر با یک مقدار باشند، پس آن دو نیز با هم برابر می شوند.] دانش آموزان را هدایت کنید تا روی پرسش 5 کار کنند و در مورد پاسخ های خود با هم گروهی شان بحث کنند. پس از اتمام وقت، از آن ها بخواهید تا معادله هایی را که نوشته اند تحویل دهند. معادله ها را بر روی تخته یا پروژکتور بنویسید.

برای دانش آموزان توضیح دهید که دیگر در رابطه ی حاصل در پرسش 5، عبارت k ظاهر نشده است. از آن ها بپرسید چرا؟ [این تساوی نیز، نتیجه ی اصل تساوی است.] دانش آموزان را هدایت کنید تا روی پرسش 6 کار کنند و در مورد پاسخ های خود با هم گروهی شان بحث کنند. پس از اتمام وقت، از آن ها بخواهید تا معادله هایی را که نوشته اند، تحویل دهند. معادله ها را روی تخته یا پروژکتور بنویسید. برای دانش آموزان توضیح دهید که رابطه های به دست آمده در پرسش های 5 و 6 با هم مساویند. از دانش آموزان بپرسید چرا رابطه ی پرسش 5 را به رابطه ی پرسش 6 ترجیح می دهند؟ [در رابطه ی پرسش 5، زوایا و ضلع مقابل به آن ها، با هم ظاهر می شوند.]از پرسش های 7 تا 13 نقش معلم به دستیاری تغییر می کند. در پرسش های 7 تا 13 دانش آموزان باید به صورت گروهی برای پاسخ به پرسش ها کار کنند. معلم باید در این مرحله، به همه ی گروه ها سر زده و مانند یک دستیار هم گروه، بحث میان گروه ها و پاسخ به پرسش ها را تسهیل کند. پس از اتمام این مرحله، معلم باید نقش ارتباط دهنده را ایفا کند. دانش آموزان باید بتوانند اجزای مختلف قانون سینوس ها را به صورت یک کل واحد با هم متصل کنند. برای کمک به اتصال بخش های مختلف قانون سینوس ها به هم، پرسش های زیر را مطرح کنید: چرا می توان نتیجه گرفت sin B/b = sin C/c ؟ [به دلیل اصل تساوی. زیرا هر دو برابر با sin A/a هستند.] قانون سینوس ها را می توان به این صورت نوشت: sin A/a = sin B/b = sin C/c. چگونه با این رابطه، می توانیم روابطی را که در طی درس به دست آورده ایم، توضیح دهیم؟ [هر یک از تساوی های این رابطه، یکی از روابطی است که در پرسش های برگه فعالیت به دست آمد.]بعد از آن که دانش آموزان برگه ی فعالیت قانون سینوس ها را کامل کردند، از آن ها بخواهید تا با استفاده از این قانون، مقادیر C ، b و c را در مثلثی که در ابتدای کلاس بحث شد، پیدا کنند. زمانی که دانش آموزان از قانون سینوس ها استفاده می کنند، نقش معلم دوباره دستیاری است. زمانی که دانش آموزان روی مسئله کار می کنند تا مقادیر مجهول را بیابندد، معلم باید به همه ی گروه ها سر بزند. پس از اتمام وقت، از یکی از آن ها بخواهید تا پای تخته، مسئله را حل کند.

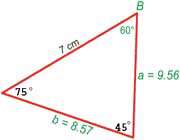
راه حل مسئله، در بالا آورده شده است. مقدار زاویه ی B را می توان با تفریق مجموع دو زوایه ی معلوم از 180 به دست آورد. اندازه ی ضلع a و b را نیز می توان با کمک قانون سینوس ها به دست آورد. پس از آن که دانش آموزان قانون سینوس ها را بسط دادند، در این مرحله باید با کاربردها و محدودیت های آن آشنا شوند. در این مرحله، معلم باید نقش پرسش کننده را ایفا کند. اشاره کنید که در مثلثی که در ابتدای کلاس بحث شد، اندازه ی دو زاویه و ضلعی که بین آن دو نیست، معلوم است. بنابراین در این حالت، یعنی حالت (ز ز ض)، می توان از قانون سینوس ها برای تعیین اندازه ی زاویه و ضلع مجهول استفاده کرد و از آن جا که (ز ز ض) یکی از حالت های تساوی دو مثلث است، پس این مثلث یکتا است. پرسش های زیر را مطرح کنید: به جز حالت (ز ز ض)، در کدام حالت های دیگر می توان از قانون سینوس ها برای تعیین اندازه زاویه و ضلع مجهول در مثلث استفاده کرد؟ [(ز ض ز)، دو زاویه و ضلع بین آن ها و (ض ض ز)، دو ضلع و زاویه ای که بین آن ها نیست.] در کدام یک از حالت های (ز ض ز) و (ض ض ز)، تنها یک مثلث با اطلاعات معلوم وجود دارد؟ چرا؟ [حالت (ز ض ز) نیز یکی از حالت های تساوی مثلث ها است؛ بنابراین ثابت می کند یک مثلث با این اطلاعات موجود است. ولی، (ض ض ز) حالت تساوی دو مثلث نیست، زیرا اطلاعات کافی برای اثبات تساوی دو مثلث در اختیار قرار نمی دهد و نمی توان از آن برای اثبات یکتایی مثلث استفاده کرد.]در انتهای کلاس، اهمیت قانون سینوس ها یعنی کاربرد آن را برای حل مسائل مثلث های غیر قائم الزاویه بیان کنید. با این حال ت?کید کنید که با قانون سینوس ها نمی توان همه ی مسائل مثلث های غیر قائم الزاویه را حل کرد. اگر دو زاویه و یک ضلع یا دو ضلع و زاویه ای به جز زاویه ی بین این دو ضلع در یک مثلث معلوم باشد، می توان از قانون سینوس ها برای تعیین زوایا و اضلاع مجهول استفاده کرد. ولی اگر دو ضلع و زاویه ای که بین آن ها نیست، معلوم باشد، زاویه و اضلاع مجهول ممکن است یکتا نباشد. پرسش هایی برای دانش آموزاناطلاعات زیر داده شده است:

آیا با اندازه ی اضلاع و زوایای داده شده، تنها یک مثلث وجود دارد؟ چرا؟[بله. زیرا (ز ز ض) یکی از حالت های تساوی دو مثلث است. بنابراین، اگر دو زاویه و یک ضلع معلوم باشد، آن مثلث یکتا است.]دو رابطه ی زیر، معادل هستند.

چرا ممکن است یکی از این رابطه ها به دیگری ترجیح داده شود؟[در رابطه ی دوم، زوایا و اضلاع روبروی هم اند؛ به همین دلیل ممکن است به رابطه ی اول ترجیح داده شود. ولی اگر مقادیر رابطه ها مشخص باشند، فرقی نمی کند از کدام یک استفاده کنید.] اگر در یک مثلث دو زاویه و ضلعی که بین آن ها نیست، معلوم باشد، قانون سینوس ها را می توان برای تعیین اندازه ی زاویه و ضلع مجهول به کار برد. در چه حالت های دیگری می توان از قانون سینوس ها برای تعیین اندازه ی زاویه و ضلع مجهول استفاده کرد؟(ز ض ز)، دو زاویه و ضلع بین آن ها و (ض ض ز)، دو ضلع و زاویه ای که بین آن ها نیست.]از حالت های (ز ض ز) و (ض ض ز)، کدام یک نشان می دهد مثلث یکتا است؟ [(ز ض ز) حالتی است که نشان می دهد مثلث یکتا است، زیرا از این حالت می توان برای اثبات تساوی دو مثلث بهره گرفت. ولی (ض ض ز) نشان دهنده ی مثلث یکتا نیست، زیرا از حالت های تساوی دو مثلث نیست و اطلاعات کافی برای تساوی دو مثلث در اختیار قرار نمی دهد.] ارزشیابی1- مجموعه ای از مثلث های مختلف با زاویه ها و اضلاع معلوم تهیه کنید. از دانش آموزان بخواهید تا تعیین کنند در کدام یک برای تعیین زاویه یا ضلع مجهول، می توان از قضیه ی سینوس ها استفاده کرد؟ از آن ها بخواهید دلیل پاسخ خود را توضیح دهند. 2- از دانش آموزان بخواهید اندازه ی ضلع یا زوایه ی مجهول مثلث های سؤال 1 را که قانون سینوس ها را می توان در آن به کار برد، پیدا کنند. توسعهبسط و توسعه ی این درس، در مورد حالت دو ضلع و زاویه ی مجاور به یکی از این اضلاع که قانون سینوس ها را می توان در آن به کار برد، است. البته هیچ تضمینی نیست که در این حالت تنها یک مثلث یکتا داشته باشید. به مثلث ABC توجه کنید.
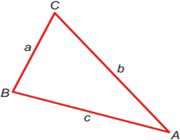
1- قانون سینوس ها را برای تعیین زاویه و ضلع مجهول به کار ببرید، اگر: B=10 و a=24 و m<A=41° باشد.[تنها یک مثلث با این مشخصات وجود دارد. اگر چه دو مقدار °15.86 و °164.14 برای زاویه ی B به دست آمد اما جواب دوم غیر قابل قبول است. بنابراین c=30.63 و °m<c=123.14 و m<b =15.86°.]2- قانون سینوس ها را برای تعیین زاویه و ضلع مجهول به کار ببرید، اگر: b=9.2 و a=6.5 وباشد m<A=32°.[با این مشخصات، دو مثلث وجود دارد؛ چون هر دو مقدار 48.59 و 131.41 درجه برای زاویه ی B قابل قبول است. اگر m<B = 48.59° پس m<C = 99.41° و c = 12.1. اگر m<B = 131.41° پس m<C = 16.59° و c = 3.5.]3- قانون سینوس ها را برای تعیین زاویه و ضلع مجهول به کار ببرید، اگر: m<B = 58°, a = 5 و b = 3.4 باشد.[این مسئله راه حلی ندارد؛ چون طبق قانون سینوس ها sin A = (5 × sin 58°) / 3.4 = 1.2471 که امکان پذیر نیست.] بررسی اجرای طرح درس در کلاسعکس العمل دانش آموزان به نقش های مختلفی که برای تدریس ایفا کردید، چه بود؟ چه روش هایی پیشنهاد می کنید تا دانش آموزان به طور فعال در این درس شرکت کنند؟آیا به نظرتان لازم است تغییراتی در شیوه ی ارائه ی این درس داده شود؟ اگر پاسختان مثبت است، چه تغییراتی و در چه قسمتی مؤثرتر است؟چه کارهایی با توجه به مدیریت رفتار در کلاس انجام شد؟ چه کارهایی انجام نشد؟ چگونه می توان کارهایی را که انجام نشد، تغییر داد؟ مترجم: راضیه کریمی
این صفحه را در گوگل محبوب کنید
قانون سینوس ها-قانون سینوس هااهدافدانش آموزان بعد از این درس می توانند:با استفاده از مثلثات مثلث قائم الزاویه، قانون سینوس ها را بسط دهند. با استفاه از قانون سینوس ...
قانون سینوس ها و کسینوس ها-قانون سینوس ها و کسینوس هادر این درس، دانش آموزان با قانون سینوسها و کسینوسها آشنا شده و یاد می گیرند که برای یافتن طول ضلع یا ...
از قانون کسینوس ها برای حل مسائل استفاده کنند. وسابل لازمبرگه ی فعالیت قانون کسینوس ها طرح درسشاید پیش از این، دانش آموزان از قانون سینوس ها تنها برای حل ...
2- دستکم یک زاویه، زاویهی باز است. 3- هیچ کدام از زاویهها، زاویهی قائمه نیستند. 4- دست کم یک زاویه، زاویهی حاده است. ... قانون سینوس ها از دانش آموزان بخواهید تا درباره ی ...
بعد از آن که دانش آموزان برگه ی فعالیت قانون سینوس ها را کامل کردند، از آن ها بخواهید تا با استفاده از این قانون، مقادیر C ، b و c را در مثلثی که در ابتدای کلاس بحث شد، ...
کاربرد مثلثات در تعیین موقعیت:زاویه ی بلندی (برگه ی 2)این فعالیت شامل یک مسئله ی مربوط به مثلثات در مثلث قائم الزاویه و یکی دیگر مربوط به قانون سینوس ها ...
افرادي كه سرما خورده اند · قانون سینوس ها و کسینوس ها · درمان کم خونی زنان با تغذيه مناسب · مشاهده و اجرای فایلهای فلش با Adobe Flash Player 10.0.45.2 ... . گوناگون ...
سینوزیت به التهاب مخاط سینوسهای هوایی گفته میشود.این سینوسها حفراتی بسته هستند كه در استخوانهای سر و اطراف حفره بینی قرار دارند. به طور كلی ما در هر طرف ...
علا وه بر بخور درمانی، آنتی بیوتیک ها که در درمانگاه ها انجام می دادند اسانس هایی نیز برای باز ... و فروکش نمودن التهاب سینوس ها به کار می آمد که معروف ترین آنها اسانس نعناع بود. ... در تمام پنج جلد کتاب قانون ابن سینا که پایه و اساس آن بر گیاهان داروئی ...
این گفته ها تا چه حد صحت دارند؟ ... این گفته ها تا چه حد صحت دارند؟ ... که خط چشم می تواند به سینوس ها راه پیدا کرده و مشکل ساز شده و سینوسها عفونی شوند وجود دارد ... صحیح تر است که قانون پنج ثانیه ای برای غذا هایی كه بر زمین می افتند را رعایت کنیم ...
-














