محبوبترینها
از کجا بفهمیم قاشق چنگال اصل است | قاشق چنگال تقلبی نخرید!
با چاپ روی وسایل یک کسب و کار پرسود بسازید
قیمت دیگ بخار و تولیدکننده اصلی دیگ بخار
معروف‌ترین هدیه و سوغاتی یزد مشخص شد!
آشنایی با انواع دوربین مداربسته ضد آب
پرداخت اینترنتی قبوض ساختمان (پرداخت قبض گاز، برق و آب)
بهترین دوره آموزش سئو محتوا در سال 1403 با نام طوفان ۱۴۰۳ در فروردین ماه شروع می شود
یک صرافی ارز دیجیتال چه امکاناتی باید داشته باشد؟
تعمیرگاه مجاز تعمیر ماشین لباسشویی در شرق تهران
تعمیرگاه مجاز تعمیر ماشین لباسشویی در شرق تهران
جراحی و درمان ریشه دندان عفونی با خانم دکتر صفوراامامی
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1799019326
پیشینه تابع
واضح آرشیو وب فارسی:فان پاتوق: پیشینه تابع «تابع»، به عنوان تعریفی در ریاضیات، توسط گاتفرید لایبنیز در سال 1694، با هدف توصیف یک کمیت در رابطه با یک منحنی به وجود آمد، مانند شیب یک نمودار در یک نقطه خاص. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم، اغلب افراد این توابع در هنگام آموختن ریاضی با این گونه توابع برمی خورند. در این گونه توابع افراد میتوانند در مورد حد و مشتق صحبت کنند. چنین توابعی پایه حسابان را میسازند.
واژه تابع بعدها توسط لئونارد اویلر در قرن هجدهم، برای توصیف یک عبارت یا فرمول شامل متغیرهای گوناگون مورد استفاده قرار گرفت، مانند f(x) = sin(x) + x3.
در طی قرن نوزدهم، ریاضیدانان شروع به فرموله کردن تمام شاخههای ریاضی کردند. ویرسترس بیشتر خواهان به وجود آمدن حسابان در علم حساب بود تا در هندسه، یعنی بیشتر طرفدار تعریف اویلر بود.
در ابتدا، ایده تابع ترجیحاً محدود شد. برای ژوزف فوریه مدعی بود که تمام توابع از سری فوریه پیروی میکنند در حالی که امروزه هیچ ریاضیدانی این مطلب را قبول ندارد. با گسترش تعریف توابع، ریاضیدانان توانستند به مطالعه «عجایب» در ریاضی بپردازند از جمله این که یک تابع پیوسته در هیچ مکان گسستنی نیست. این توابع در ابتدا بیان نظریههایی از روی کنجکاوی فرض میشد و آنها از این توابع برای خود یک «غول» ساخته بودند و این امر تا قرن بیستم ادامه داشت.
تا انتهای قرن نوزدهم ریاضیدانان سعی کردند که مباحث ریاضی را با استفاده از نظریه مجموعه فرموله کنند و آنها در هر موضوع ریاضی به دنبال تعریفی بودند که از مجموعه استفاده کند. دیریکله و لوباچوسکی هر یک به طور مستقل و تصادفاً هم زمان تعریف «رسمی» از تابع دادند.
در این تعریف، یک تابع حالت خاصی از یک رابطه است که در آن برای هر مقدار اولیه یک مقدار ثانویه منحصر به فرد وجود دارد.
تعریف تابع در علم رایانه، به عنوان حالت خاصی از یک رابطه، به طور گستردهتر در منطق و علم تئوری رایانه مطالعه میشود.
توابع در سایر علوم
توابع مورد استفاده در اکثر علوم کمی میباشند، برای مثال در فیزیک، هنگامی که میخواهیم رابطه بین چند متغیر را بیان کنیم، مخصوصاً در زمانی که مقدار یک متغیر کاملاً وابسته به متغیر دیگر است. برای مثال وقتی که میخواهیم نشان دهیم که تغییر دمای آب چه تاثیری بر روی چگالی آن میگذارد.
توابع را همچنین مورد استفاده در علم رایانه برای مدلسازی ساختمان دادهها و تاثیرات الگوریتم میبینیم. این کلمه در رویهها و زیرروالها بسیار دیده میشود.
اصطلاحات توابع
به یک مقدار ورودی مشخص در یک تابع، آرگومان تابع میگویند. برای هر آرگومان x، مقدار منحصر به فرد y در مجموعه اعداد برد تابع وجود دارد که با آن مطابقت میکند، و به آن مقدار در x یا تصویر x تحت f میگویند. تصویر x میتواند با (f(x و یا y نشان داده شود.
گراف تابع f مجموعه تمام زوج مرتبهای ((x, f(x) به ازای تمام xهای درون دامنه X است. اگر X و Y زیرمجموعههایی از R (اعداد حقیقی) باشند، در این صورت این تعریف مانند شهود «گراف» به عنوان یک تصویر یا نمودار تابع به همراه زوج مرتبهای نقاط در محور مختصات است.
مفهوم تصویر را میتوان اتصال مجموعهای از نقاط تصویر به هم دانست. اگر A زیرمجموعهای دامنه باشد، آن گاه (f(A هم زیرمجموعهای از برد است که شامل تمام تصویرهایهای مقادیر A میشود. در این صورت میگوییم که (f(A تصویر A تحت f است.
به یاد داشته باشید که برد f همان تصویر (f(X در مقادیر دامنهاست و برد f زیرمجموعهای از مجموعه تمام مقادیر ممکن برای f است.
وارون (یا معکوس) مجموعه B که مجموعه مقایر ممکن برای Y تحت تابع f است زیرمجموعهای از دامنه X است که به این صورت تعریف میشود:
f −1(B) = {x in X | f(x) is in B}
برای مثال، وارون مجموعه {4, 9} تحت تابع مربع مجموعه {−3,−2,+2,+3} است.
به طور کلی، وارون یک نقطه منحصر به فرد (نقطهای که فقط یک مقدار برای آن وجود داشته باشد)، میتواند مجموعه تمام اعداد را دربرگیرد. برای مثال اگر f(x) = 7 باشد، آن گاه وارون {5} تهی است اما وارون {7} برابر مقادیر دامنه آن است. در این صورت وارون یک مقدار در برد زیرمجموعهای از دامنه آن است. طبق قرارداد وارون یک مقدار یعنی f −1(b) ویا همان f −1({b}) به صورت زیر است:
f −1(b) = {x in X | f(x) = b}
مهمترین توابع عبارتند از: تابع یکبهیک، که در آن این خاصیت وجود دارد که اگر f(a) = f(b) باشد آن گاه a هم باید با b برابر باشد. تابع پوشا، که در آن این خاصیت وجود دارد که برای هر y در برد، یک مقدار x در دامنه وجود داشته باشد یعنی f(x) = y. توابعی که هم یکبهیک و هم پوشا هستند. اگر از تعریف اول تابع که در بالا گفته شد استفاده شود، تا موقعی که برد تعریف نشده باشد، «یکبهیک» بودن تابع باید وضعیتی مانند پوشا بودن را داشته باشد. میتوان از ترکیب دو یا چند تابع به عنوان یک تابع استفاده کرد. برای مثال، f(x) = sin(x2) ترکیب یک تابع سینوسی و یک تابع درجه دو است. توابع f: X → Y و g: Y → Z میتوانند با هم ترکیب شوند، به طوری که ابتدا این عمل بر روی تابع f انجام شود و y = f(x) به دست آید و یک بار هم بر روی g اعمال شود و z = g(y) به دست آید. تابع مرکب g و f به صورت زیر نوشته میشود:
ابتدا تابع سمت راست عملیات را انجام میدهد و سپس تابع سمت چپ (برعکس زبان انگلیسی) و این تابع را «جیاُاِف» میخوانیم.
در تعریفی غیرعلمی، تابع وارون f تابعی است که اثر تابع f را خنثی کند، به این صورت که هر مقدار (f(x را به آرگومان x نسبت دهد. تابع مربع (درجه دو) وارون تابع غیرمنفی جذر (ریشه دوم) است، به طوری که اگر f دارای دامنه X و برد Y و گراف G باشد، آن گاه وارون آن دارای دامنه Y و برد X و گراف است.
G−1 = { (y, x) : (x, y) ∈ G }
برای مثال اگر گراف f برابر G = {(1,5), (2,4), (3,5)} باشد، آن گاه گراف f−1 برابر G−1 = {(5,1), (4,2), (5,3)} میشود.
رابطه f−1 یک تابع است اگر و تنها اگر برای هر y در برد فقط یک آرگومان x مانند f(x) = y وجود داشته باشد، به عبارت دیگر، وارون تابع f یک تابع است اگر و تنها اگر f پوشا و یکبهیک باشد. در این مثال، برای هر x درون X f−1(f(x)) = x و برای هر y درون Y f(f−1(y)) = y است. گاهی اوقات میتوان یک تابع را تغییر داد و این کار اغلب با جایگذاری دامنهای جدید که زیرمجموعهای از دامنه قبلی باشد صورت میگیرد، و همینطور باید تغییرات را در برد و گراف اعمال کرد که در این صورت تابع تغییر داده شده دارای وارونی است که خود یک تابع است.
برای مثال وارون تابع y = sin(x)، یعنی f(x) = arcsin (x)، به صورت y = arcsin (x) تعریف میشود اگر و تنها اگر x = sin(y) باشد، و این یک تابع نیست زیرا گراف آن شامل دو زوج مرتب (0, 0) و (0, 2π) است. اما اگر دامنه y = sin(x) را به −π/2 ≤ x ≤ π/2 تغییر دهیم، برای برد داریم −1 ≤ y ≤ 1 و در این صورت وارون تابع مورد نظر یک تابع است، و برای بیان آن از A در حرف اول آن استفاده میکنیم، یعنی (f(x) = Arcsin (x.
اما این روش برای همه توابع عملی نیست، زیرا در بعضی موارد پیدا کردن وارون توابع غیرممکن است.
مشخص کردن تابع
اگر دامنه X تعریف شده باشد، تابع f را میتوان با جدولبندی کردن آرگومانهای x و جواب آنها در f(x) تعریف کرد.
چیزی که برای تعریف کردن تابع رایجتر است استفاده از فرمول و به طور کلی استفاده از الگوریتم است، که در آن نشان داده میشود چه عملیاتی باید بر روی xهای دامنه انجام گیرد تا f(x) به دست آید. برای تعریف یک تابع میتوان از عمل ریاضی که با آرگومان x رابطهای داشته باشد استفاده کرد. البته راههای زیاد دیگری برای تعریف یک تابع وجود دارد؛ از جمله استفاده از روش بازگشتی، استفاده از بسطهای تجزیه و عبارات جبری، حدها، دنبالهها، سریها و استفاده از معادلات دیفرانسیل.
در ریاضیات توابع زیادی وجود دارد که نمیتوانند مفهوم خود را به طور دقیق برسانند. یکی از نتایج اصلی نظریه شمارش این است که توابع زیادی وجود دارند که تعریف میشوند اما قابل محاسبه نیستند.
علامت تابع
معمولاً پرانتزهای کنار آرگومان را هنگامی که برای آن ابهامی وجود ندارد حذف میکنند، مانند: sin x. در برخی موارد علمی، از علامت نشانگذاری لهستانی معکوس استفاده میشود، که با این کار باید پرانتزها را حذف کرد؛ و برای مثال تابع فاکتوریل همواره به صورت n! نوشته میشود، در حالی که اکثر افراد تابع گاما را به صورت (Γ(n مینویسند.
برای نشان دادن یک تابع ابتدا نام آن را میآوریم، سپس دامنه، بعد برد و در انتها هم ضابطه تابع را مینویسیم. با استفاده از این روش اغلب تابع به دو قسمت نشان داده میشود، مانند:
در اینجا دامنه تابع با نام «f» اعداد طبیعی و برد آن اعداد حقیقی است، و n را به خودش تقسیم بر π تبدیل میکند. (در بعضی موارد نام تابع را به همراه دونقطه، در بالای پیکان میآورند). روش نشان دادن دیگری هم وجود دارد که رایجتر اما غیرعلمیتر است، در این روش تابع به شکل کوتاه شده زیر نشان داده میشود:
در این روش اطلاعات کمتری ارائه شدهاست و ما از دامنه و برد تابع خبر نداریم، و در این صورت به جای n میتوانیم هر عددی از قبیل اعداد گنگ هم قرار دهیم.
بعضی از نویسندگان به جای استفاده از (f(A از [f[A استفاده میکنند و این کار برای رفع ابهام میان دریافت مفاهیم است، بعضی دیگر هم از f`x به جای (f(x، و f``A به جای [f[A استفاده میکنند.
توابع با چند ورودی و خروجی
توابع دو (یا چند) متغیره
مفهوم تابع را میتوان با ترکیب دو یا چند آرگومان بیان کرد. این مفهوم شهودی، زمانی میتواند تعریف شود که دامنه تابع حاصلضرب دکارتی دو یا چند مجموعه باشد.
برای مثال، عملیات را بر روی تابع ضربی که از دو عدد صحیح برای به دست آوردن حاصل استفاده میکند انجام میدهیم: f(x, y) = x·y. تابع میتواند دامنه Z×Z، مجموعه تمام زوجها به عنوان برد Z، و برای گراف، مجموعه تمام زوجهای ((x,y), x·y) را داشته باشد. به یاد داشته باشید که مولفه اول چنین زوجهایی یک زوج از اعداد صحیح است، در حالی که مولفه دوم تنها یک عدد صحیح است.
مقدار تابع زوج (x,y) برابر است با f((x,y)). اگر چه معمولاً یک جفت از پرانتزها را حذف میکنند و آن را به شکل f(x,y) نشان میدهند، یعنی یک تابع دومتغیره شامل x و y.
توابعی که حاصلشان یک مجموعه ضرب است
در این گونه توابع، مقدار تابع شامل چند متغیر است. برای مثال، تابع mirror(x, y) = (y, x) را با دامنه R×R و برد R×R در نظر بگیرید. زوج (y, x) یکی از مقادیر برد تابع که یک مجموعهاست، میباشد.
عملیات دوتایی
منظور ار عملیات دوتایی ساده در ریاضی همان جمع و ضرب است، وقتی که در توابع استفاده شوند مقادیر را از Z×Z به Z میبرند. این موضوع در جبر شرح داده میشود و در آنجا از توابع nتایی برای انجام عملیات استفاده میشود.
چیزی که از گذشته مورد استفاده قرار میگرفته این است که از عملیات جمع و ضرب به عنوان نشانههای میانوندی استفاده شود: x+y و x×y به جای +(x, y) و ×(x, y).
مجموعه توابع
مجموعه یک تابع از یک مجموعه X به یک مجموعه Y به صورت X → Y یا [X → Y] یا YX نشان داده میشود. آخرین عبارت یاد شده با استفاده از قضیه بدیهی |YX| = |Y||X| اثبات میشود. جزئیات بیشتر در اعداد اصلی بیان شدهاست.
معمولاً از عبارت f: X → Y برای بیان f ∈ [X → Y] استفاده میشود، و «f تابعی از X به Y است» خوانده میشود. بعضی افراد هم آن را «f: X → Y» مینویسند.
آیا یک تابع بیشتر از گرافش است؟
بعضی از ریاضیدانان از یک رابطه دوتایی (از اینجا به بعد آن را تابع میگوییم) به عنوان سهتایی مرتب (X, Y, G) استفاده میکنند، که در آن X و Y مجموعه دامنه و برد، و G گراف f است. اگر چه، سایر ریاضیدانان رابطهای را تعریف میکنند که فقط شامل زوجهای مجموعه G باشد، بدون این که دامنهای برای آن تعیین کرده باشند.
در هر تعریف خوبیها و بدیهایی وجود دارد، اما هر یک از آنها تعاریف مناسبی هستند که مورد استفاده در ریاضی قرار میگیرند. دامنه و برد موضوع مهمی است و باید به طور واضح مشخص باشند.
توابع ناقص و توابع چندتایی
وضعیت یک رابطه دوتایی f از X به Y را میتوان به دو صورت تقسیم نمود: f تابع جمعی: برای هر x در X، چند y در Y وجود دارد به طوری که x با y در رابطه باشد. f تابع تک-مقداری باشد: برای هر x در X، حداقل یک y در Y وجود دارد به طوری که x با y در رابطه باشد.
جمعی و نه تک-مقداری
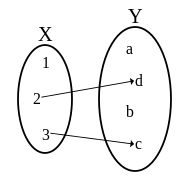
تک-مقداری و نه جمعی
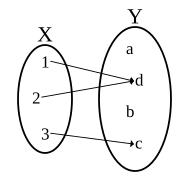
تک-مقداری (یک تابع)
در بعضی موارد که تابع وضعیت اول را دارد اما لزوماً از وضعیت دوم پیروی نمیکند، میتوان تابع را تابع چندارزشی خواند؛ و رابطهای که وضعیت دوم را دارد اما لزوماً از وضعیت اول پیروی نمیکند را میتوان تابع ناقص خواند
-
این صفحه را در گوگل محبوب کنید
[ارسال شده از: فان پاتوق]
[مشاهده در: www.funpatogh.com]
[تعداد بازديد از اين مطلب: 467]
-
گوناگون
پربازدیدترینها