تبلیغات
تبلیغات متنی
محبوبترینها
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
پروازهای مشهد به دبی چه زمانی ارزان می‌شوند؟
تجربه غذاهای فرانسوی در قلب پاریس بهترین رستوران‌ها و کافه‌ها
دلایل زنگ زدن فلزات و روش های جلوگیری از آن
خرید بلیط چارتر هواپیمایی ماهان _ ماهان گشت
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1836823791
الگوریتم RSA
واضح آرشیو وب فارسی:راسخون:
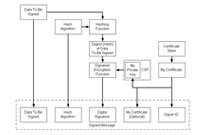
الگوریتم RSA الگوریتم RSA پس از آنکه ران ریوست (Ron Rivest)، آدام شامیر (Adam Shamir) و لن ادلمن (Len Adleman) در سال ۱۹۷۷ آنرا بدست آوردند به این نام مشهور شد، هرچند تکنیک های اولیه آن پیشتر در سال ۱۹۷۳ توسط فردی بنام کلیفورد کوکس (Clifford Cocks) بدست آمده بود اما تا سال ۱۹۷۷ اولا” الگورتیم کاملا” محرمانه بود و ثانیا” به سادگی آنچه در زیر بیان خواهیم کرد نبود.تهیه کلید های عمومی و خصوصیبطور خلاصه روش کار برای تهیه کلیدها به شرح زیر است :۱- دو عدد بزرگ (هر چه بزرگتر بهتر) اول به نام های p و q را انتخاب می کنیم، بهتر است این اعداد از لحاظ سایز نزدیک به یکدیگر باشند.۲- عدد دیگری بنام n را معادل با حاصلضرب p در q تعریف می کنیم : n = p x q۳- عدد چهارم یعنی m را معادل حاصلضرب p-۱ در q-۱ تعریف می کنیم : (m = (p-۱) x (q-۱۴- عدد e را که از m کوچکتر است آنگونه پیدا می کنیم که بزرگترین مقسوم علیه مشترک این دو یک باشد به عبارتی نسبت به هم اول باشند.۵- عددی مانند d را پیدا کنید که باقیمانده حاصلضرب d در e تقسیم بر m مساوی عدد ۱ باشد، یعنی : d x e) mod m = ۱)حال پس از طی این مراحل شما می توانید از e و n بعنوان کلید عمومی و از d و n بعنوان کلید اختصاصی استفاده کنید.روش پنهان کردن و آشکار کردنبرای کد کردن اطلاعات کافی است عدد منتصب به هر کاراکتر - مثلا” ASCII - را که در اینجا M می نامیم در فرمول زیر قرار دهید و بجای ارسال آن عدد C = Me mod n را ارسال کنید. در واقع دراینجا شما توانسته اید با کمک کلید عمومی، کاراکتر M را به C تبدیل کنید.حال گیرنده برای آشکار سازی کافی است عدد دریافتی یعنی C را با استفاده از کلید خصوصی به M تبدیل کند. برای اینکار کافی است از این فرمول استفاده کنید : M = Cd mod n ، بنابراین شما با دریافت کاراکتر کد شده C و در دست داشتن کلید خصوصی توانسته اید کاراکتر اصلی را مشخص نمایید. یک مثال:با توجه به روشی که در مطلب قبل ارایه کردیم در اینجا بعنوان نمونه مثالی از نحوه تعریف کلید های عمومی و خصوصی خواهیم آورد. اما برای سادگی محاسبات از اختیار کردن اعداد بزرگ دوری خواهیم کرد و توجه شما را به این نکته جلب می کنیم که هرچقدر اعداد اولیه بزرگتر باشند احتمال شکستن رمز در مدت زمان محدود ناچیزتر می شود.۱- ابتدا باید دو عدد اول بزرگ انتخاب کنیم که در اینجا از اعداد ساده و هم اندازه ای مانند ۱۱ و ۳ استفاده می کنیم. پس p=۱۱ , q=۳۲- حاصلضرب p در q که همان n است را به اینصورت خواهیم داشت : n = ۱۱ x ۳ = ۳۳۳- حاصلضرب p-۱ در q-۱ که همان m است را به اینصورت خواهیم داشت : m = ۱۰ x ۲ = ۲۰۴- برای انتخاب عدد e که نسبت به m=۲۰ اول باشد و کمتر از آن هم باشد ساده ترین گزینه یعنی عدد ۳ را انتخاب می کنیم.۵- برای یافتن عدد d که در رابطه d x e) mod m = ۱) صادق باشد اعداد ۱,۲,۳,۴,۵ و … را امتحان می کنیم، بنظر می رسد که عدد ۷ برای اینکار مناسب باشد چرا که ۷×۳=۲۱ باقیمانده ای معادل ۱ بر m=۲۰ دارد.حال می توانیم از زوج (۳۳,۳) بعنوان کلید عمومی و از زوج (۳۳,۷) بعنوان کلید خصوصی استفاده کنیم. حال اگر از فرمول هایی که در مطلب قبل برای کد کردن و آشکار سازی استفاده کنیم برای اعداد ۱ تا ۱۶۳۲ به جدول زیر خواهیم رسید.m ۰۱۲۳۴۵۶۷۸۹۱۰۱۱۱۲۱۳۱۴۱۵۱۶c ۰۱۸۲۷۳۱۲۶۱۸۱۳۱۷۳۱۰۱۱۱۲۱۹۵۹۴m ۱۷۱۸۱۹۲۰۲۱۲۲۲۳۲۴۲۵۲۶۲۷۲۸۲۹۳۰۳۱۳۲c ۲۹۲۴۲۸۱۴۲۱۲۲۲۳۳۰۱۶۲۰۱۵۷۲۶۲۵۳۲بنابراین هم اکنون شما یک جدول تبدیل کد دارید که با کمک کلید عمومی اعداد صفر تا ۳۲ را به اعدادی کد شده و در همین رنج تبدیل کرده اید. اما اگر دقت کنید تعدادی از اعداد دقیقا” به همان عدد خود تبدیل شده اند که به اینها unconcealed یا مخفی نشده گفته می شود. اولآ باید بدانیم که ۰ و ۱ همواره به همین اعداد تبدیل می شوند و مطلب دیگر اینکه اگر رنج دو عدد اول ابتدایی را بزرگ در نظر بگیریم دیگر مشکلی پیش نخواهد آمد. حال کافی است فرض کنیم A=۲ ، B=۳ ، C=۴ و … Z=۲۷ و جملات مربوطه را کد نماییم. دقت کنید که معمولا” از ۰ و ۱ برای کدینگ استفاده نمی شود.منبع:http://www.academist.ir/خ
این صفحه را در گوگل محبوب کنید
[ارسال شده از: راسخون]
[مشاهده در: www.rasekhoon.net]
[تعداد بازديد از اين مطلب: 5221]
-
گوناگون
پربازدیدترینها