محبوبترینها
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1846032659
دست دادن ها در کلاس
واضح آرشیو وب فارسی:تبیان: دست دادن ها در کلاساهداف- دانش آموزان خواهند توانست پاسخ تعمیم یافته ی مسئله ی دست دادن ها را توضیح دهند.- دانش آموزان خوا هند فهمید که مسئله ی دست دادن ها غیر خطی است. وسایل لازم- برگه ی فعالیت دست دادن ها - کاغذ شطرنجی - طرح آموزشی درس اول در این درس، دانش آموزان مسئله ی دست دادن را بررسی می کنند. این مسئله یک مسئله ی کلاسیک ریاضی است و به این صورت است که وقتی n نفر با هم دست می دهند، چه تعداد دست دادن اتفاق می افتد؟ گروه ها تعیین می کنند که چه تعداد دست دادن در بین دانش آموزان یک کلاس اتفاق می افتد و سپس این راهکار را برای هر گروه با هر تعداد افراد تعمیم می دهند. دانش آموزان مسئله را با استفاده از توضیحات شفاهی، جدول، نمودار، عکس و فرمول جبری بررسی می کنند. در این تحقیق، دانش آموزان مسئله ی قدیمی دست دادن ها را حل خواهند کرد. این مسئله می تواند به صورت زیر مطرح شود: وقتی افراد یک گروه n نفره، با هر نفر در این گروه دقیقاً یک بار دست می دهند، چه تعداد دست دادن انجام می شود؟ دانش آموزان این مسئله را با استفاده از نمایش های متعددی بررسی می کنند: با استفاده از نمایش واقعی (انجام دست دادن ها و شمارش آن ها)، تصویر، جدول مقادیر، نمودار و فرمول جبری. ابتدا یکی از روش ها برای حل مسئله انتخاب می شود و سپس، دانش آموزان قبل از این که پاسخ هایشان را برای کلاس توضیح دهند، مسئله را از راه های دیگری بررسی می کنند. سپس، مسئله را به صورت زیر برای دانش آموزان مطرح کنید: در کلاسی 9 دانش آموز وجود دارد. اگر هر یک از آن ها با همدیگر فقط یک بار دست دهند، چه تعداد دست دادن اتفاق می افتد؟ شما ممکن است بخواهید که متن این مسئله را روی تخته یا با استفاده از پروژکتور برای دانش آموزان نمایش دهید. دانش آموزان را به گروه های 4 نفری تقسیم کنید و از آن ها بخواهید تا تعداد دست دادن هایی را که دریک گروه 9 نفره اتفاق می افتد، پیدا کنند. به دانش آموزان اطلاع دهید که پاسخ هایشان را باید در کلاس ارائه دهند. بنابراین بهتر است پاسخ هایشان را روی کاغذ ثبت کنند. با طرح مساله ی ساده تری، آن ها را راهنمایی کنید. برای مثال، می توانید بپرسید: در گروهتان، چه تعداد دست دادن می تواند رخ دهد؟ به دانش آموزان کمک کنید تا مسئله را با دست دادن با یگدیگر، مدل سازی کنند. انجام این عمل به طور عینی می تواند گروه ها را تشویق کند تا تعداد دست دادن ها را برای بیشتر از 4 نفر نیز پیدا کنند. مسئله ی یافتن تعداد دست دادن ها در یک گروه 9 نفری، راه خوبی برای معرفی مسئله است اما ارزش حقیقی مسئله در این است که از دانش آموزان بخواهیم نتایج خود را تعمیم دهند. از دانش آموزانی که جواب مسئله را برای 9 نفر پیدا کرده اند، بخواهید تا به فعالیت ادامه دهند و الگویی کلی را برای تعداد دست دادن ها در گروهی 8 نفره بیابند. سپس بر گه ی فعالیت دست دادن ها را توزیع کنید.
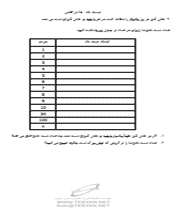
تعداد دست دادن مردم 0 1 1 2 3 3 6 4 10 5 15 6 21 7 28 8 36 9 45 10 55 11 66 12 دانش آموزان این مسئله را با استفاده از راه های متفاوتی حل خواهند کرد. به علاوه برای انجام عینی آن، می توانند از تصاویر، راه حل های هندسی و یا لیست های تعمیم یافته استفاده کنند. فهرستی در دو ستون باید ایجاد شود که اولین ستون تعداد افراد و دومین ستون تعداد دست دادن ها را نشان دهد.
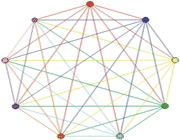
یکی از راه حل ها می تواند به این صورت باشد: هر نقطه نمایش دهنده ی یک نفر است و هر خط بین دو نقطه نشان دهنده ی دست دادن آن دو نفر است. مثلاً در شکل بالا، نفر اول (نقطه ی قرمز) با 8 نفر دست می دهد. نفر دوم (نقطه ی آبی) فقط با 7 نفر دست می دهد چون قبلاً با نفر اول دست داده است. نفر سوم (نقطه ی زرد) با 6 نفر دست می دهد چون قبلاً با نفر اول و دوم دست داده است و به همین ترتیب ادامه می یابد. یک لیست سازماندهی شده نیز می تواند همه ی دست دادن ها را نشان دهد. توجه کنید که هر جفت اعداد در جدول زیر شامل یک بار دست دادن می شود. یعنی اگر جفت 4-6 انتخاب شود، دیگر جفت 6-4 را نمی توان انتخاب کرد چون هر دو دست دادن نفر چهارم و ششم را نشان می دهد. همچنین جفت هایی با اعداد یکسان نیز حساب نمی شوند، مثل 7-7. چون آن ها نشان دهنده ی دست دادن یک نفر با خودش است. 8 بار دست زدن1-2 1-3 1-4 1-5 1-6 1-7 1-8 1-9 7 بار دست زدن2-3 2-4 2-5 2-6 2-7 2-8 2-9 6 بار دست زدند3-4 3-5 3-6 3-7 3-8 3-9 5 بار دست زدن4-5 4-6 4-7 4-8 4-9 4 بار دست زدن5-6 5-7 5-8 5-9 3 بار دست زدن6-7 6-8 6-9 2 بار دست زدن7-8 7-9 1 بار دست زدن8-9 بحث در مورد روش حل را با مدل های نمایشی شروع کنید. از 9 دانش آموز بخواهید که در یک صف در جلوی کلاس بایستند. اولین دانش آموز در طول صف حرکت می کند، با همه دست می دهد و کلاس تعداد دست دادن ها را بلندمی شمارد (8). سپس او می نشیند. دانش آموز بعدی در طول صف حرکت می کند و در حالی که کلاس با صدای بلند می شمارد، با همه دست می دهد (7). دانش آموز بعدی 6 بار دست می دهد، سپس 5، 4، 3، 2 و 1. برای دست دادن دانش آموز آخر، کسی باقی نمی ماند، چون او با همه ی دانش آموزان قبل از خود در صف دست داده است. در نتیجه، او فقط باید بشیند. جمع کل دست دادن ها برابر است با: 36 = 8+7+6+5+4+3+2+1. حالا بپرسید برای 30 نفر چه تعداد دست دادن اتفاق می افتد؟ در کل کلاس، چه تعداد دست دادن اتفاق می افتد؟ از دانش آموزان بخواهید تا به روش های حل مسئله برای گروه ها ی بزرگ تر فکر کنند. از هر گروه بخواهید که با استفاده از نمودارهایی که رسم کرده اند، راه حلشان را توضیح دهند. با دانش آموزان بحث و گفتگو کنید و از آن ها بپرسید که آیا توضیح گروهی برای گروه های دیگر منطقی است؟ راه حل این گروه چه شباهت و چه تفاوتی با گروه شما دارد؟ وقتی همه ی دانش آموزان به نتیجه ی واحدی رسیدند و قبول کردند که 9 نفر در کل 36 بار با هم دست می دهند، مسئله را گسترش دهید. بپرسید با 10 نفر چه تعداد دست دادن اتفاق می افتد؟ با استفاده از فهرست، دانش آموزان می توانند مشاهده کنند که در هر سطر یکی بیشتر از سطر قبلی اضافه می شود. بنابراین، برای 10 نفر 45 =9+36 بار دست دادن اتفاق می افتد. به دانش آموزان فرصت دهید تا برگه ی فعالیت دست دادن ها را بررسی کنند. این نمایش تعاملی باعث می شود دانش آموزان بهتر بتوانند الگوهای تعداد دست دادن هایی را که در فهرست نشان داده شده است، بررسی کنند. وقتی یک نفر به تعداد افراد اضافه می شود، دانش آموزان می توانند تغییراتی را که در تعداد دست دادن ها اتفاق می افتد، بررسی کنند. این رابطه را رابطه ی بازگشتی می گویند، چون تعداد دست دادن ها برای n نفر، می تواند بر حسب تعداد دست دادن هایی که برای (n-1) نفر اتفاق می افتد، تعریف شود. دانش آموزان ممکن است محاسبه ی تعداد دست دادن ها برای گروه های 20 نفره ییا بیشتر را نیز به راحتی بیابند. اگر دانش آموزان فکر می کنند که مسئله را حل کرده اند و دنبال تعمیم این راه حل نباشند، سؤال زیر را مطرح کنید: اگر 100 دانش آموز همدیگر را ملاقات کنند و با هم دست دهند چه تعداد دست دادن اتفاق می افتد؟ برگه ی فعالیت را توزیع کنید و به دانش آموزان فرصت دهید تا جدول را کامل و رابطه را پیدا کنند. (ممکن است بخواهید برگه ی فعالیت را به صورت اسلاید دیواری با یک ویدئو پروژکتور نمایش دهید و از کلاس بخواهید که با همکاری هم، چند سطر اول را پر کنند. از دانش آموزان مختلف بخواهید رابطه هایی را که مشاهده می کنند، توضیح دهند. از کلاس بخواهید تصمیم بگیرند که آیا با استفاده از آن رابطه می توانند تعداد دست دادن ها برای 30،100 و یا n نفر را تعیین کنند. برخی از روابط محتملی که دانش آموزان ممکن است مشاهده کنند: - تعداد نفرات قبلی را به تعداد دست دادن هایشان اضافه کنید. نتیجه ی به دست آمده تعداد دست دادن های نفرات قبلی به اضافه ی یک نفر را نشان می دهد. برای مثال، برای 4 نفر 6 دست دادن اتفاق می افتد. بنابراین برای 5 نفر 10=4+6 دست دادن وجود دارد. - اختلاف بین اعداد ستون دوم، الگوی خطی 1 و 2 و 3 و 4 و ... را تشکیل می دهد. در نتیجه ی این مشاهدات، دانش آموزان باید بفهمند که تعداد دست دادن ها برای 30 نفر برابر است با: 435=29+000+3+2+1.به همه ی پیشنهاد های دانش آموزان توجه کنید و از آن ها بخواهید تعداد دست دادن ها برای 100 نفر را بیابند. برای تعیین قاعده ایی کلی برای روابط، دانش آموزان را راهنمایی کنید و به آن ها بگویید به دنبال روابطی باشند که از عمل ضرب استفاده می شود و سؤالات زیر را مطرح کنید: - برای 7 نفر، 21 دست دادن وجود دارد. رابطه ی بین 7 و 21 چگونه است؟ (21 سه برابر 7 است.)- برای 9 نفر، 36 دست دادن وجود دارد. چه رابطه ای بین 9 و 36 وجود دارد؟ (36 چهار برابر 9 است.) - برای 8 نفر چطور؟ 28 دست دادن وجود دارد. چگونه 8 به 28 مرتبط می شود؟ (28 سه و نیم برابر 8 است.) دانش آموزان می توانند مشاهده کنند که تعداد دست دادن ها برابر است با تعداد نفرات قبلی ضرب در تعداد نفرات فعلی، تقسیم بر 2. فرمول جبری آن به صورت زیر است:
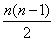
روش دیگری برای به دست آوردن فرمول بالا این است که از یک جدول سازماندهی شده استفاده کنید. اگر 9 نفر وجود دارد، می توانید افراد را در امتداد سطر بالا وستون چپ، همان طور که در زیر نشان داده شده است، مرتب کنید. داده های جدول، تعداد دست دادن ها را نشان می دهد. دست دادن ها در خانه های زرد نشان می دهد که یک نفر با خودش دست داده است، بنابراین آن ها را نباید حساب کرد. داده های خانه های قرمز همان داده ها ی خانه های آبی است. بنابراین خانه های قرمز و آبی، دست دادن های یکسانی را نمایش می دهد و فقط نصف آن ها را باید حساب کرد. برای 9نفر، 81 داده در جدول وجود دارد، ولی با توجه به توضیحات قبلی، جواب 36= 2/ (9 - 81) را می دهد. در کل برای n نفر، تعداد داده های جدول 2n است و n داده در امتداد قطر وجود دارد. بنابراین، تعداد دست دادن ها برابر است با (2/1)(n2-n) که با فرمول جبری ارائه شده در بالا معادل است.
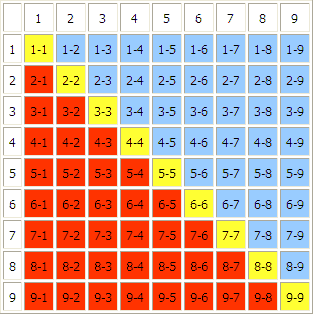
وقتی دانش آموزان به این فرمول رسیدند، از آن ها بپرسید آیا مهم است که اول ضرب انجام شود و بعد بر 2 تقسیم شود؟ آیا می توان ابتدا بر 2 تقسیم کرد و بعد عمل ضرب را انجام داد؟ (به دلیل خاصیت تعویض پذیری، ترتیب مهم نیست.) این نکته مهم است، چون دانش آموزان می توانند با استفاده از سه روش زیر، فرمول را به صورت ذهنی محاسبه کنند. - n را در (1-n) ضرب کنند و سپس بر 2 تقسیم کنند.- n را به 2 تقسیم کنند و سپس در (1-n) ضرب کنند و یا - (n-1) را بر 2 تقسیم کنند و سپس در n ضرب کنند. دانش آموزان باید با توجه به این که n زوج است یا (n-1)، تصمیم بگیرند که کدام عدد را بر 2 تقسیم کنند. به عنوان مثال، برای 15 نفر ، n-1)=14, n=15) در نتیجه منطقی است که 14 را به 2 تقسیم کنیم و سپس در 15 ضرب کنیم: 105= 7 × 15.همچنین، برای 20 نفر .n-1)=19 , n=20) در نتیجه منطقی است که 20 را به 2 تقسیم کنیم و سپس در 19 ضرب کنیم 190= 10 × 19. به عنوان مرحله ی آخر، دانش آموزان می توانند رابطه ی بین تعداد افراد و تعداد دست دادن ها را رسم کنند. دانش آموزان باید شکل نمودار را توصیف کنند و به سؤالات زیر پا سخ دهند:- آیا رابطه خطی است؟ (خیر، رابطه غیر خطی است.)- چگونه از روی جدول می فهمید که رابطه خطی نیست؟ (آهنگ تغییر ثابتی وجود ندارد.)- چگونه از روی فرمول متغیردار، می فهمید که رابطه خطی نیست؟ (متغیر n در (n-1) ضرب می شود و نتیجه شامل n2 است که نشان می دهد منحنی درجه دوم است.)- با استفاده از نمودار، چگونه پی می برید که رابطه خطی نیست؟ (نمودار یک منحنی است، نه یک خط راست.) در انتهای درس، دانش آموزان از پاسخ هایی شامل جدول، توضیح های شفاهی، نمایش تصویری و معادله ی متغیر دار استفاده خواهند کرد. مهم است که این راهکارها را به وضوح برای دانش آموزان نشان دهید تا دانش آموزان تشویق شوند که از همه ی این شیوه ها استفاده کنند. هر شیوه ای فواید خاصی دارد و می تواند بینش خوبی هنگام حل مسئله ایجاد کند. پرسش هایی برای دانش آموزاناگر هر دانش آموز با دانش آموز دیگر فقط یک بار دست دهد، چه تعداد دست دادن اتفاق می افتد؟ (با 9 دانش آموز، 36 دست دادن اتفاق می افتد.) تعداد دست دادن ها در یک گروه n نفره چقدر است؟ (در یک گروه n نفره، 1+2+3+…+n دست دادن وجود دارد که می توان به صورت 2/(n)(n-1) نوشت.) در یک گروه 40 نفره چه تعداد دست دادن وجود دارد؟ برای 100 نفر چطور؟ (با استفاده از فرمول، 780= 2/ (39×40) دست دادن در گروه 40 نفره و 4950= 2/ (99×100) دست دادن در گروه 100 نفره وجود دارد.) ارزشیابیاز دانش آموزان بخواهید پاسخ هایشان را به سوال اصلی بنویسند و نشان دهند که چگونه تعداد دست دادن ها را در هر تعداد گروه فهمیده اند؟اگر همه ی 12معلم وقتی که در جلسه شرکت می کنند، با هم دست دهند، چه تعداد دست دادن اتفاق می افتد؟ برای توضیح پاسختان از 2 روش استفاده کنید.در یک مهمانی، هر نفر با بقیه دست می دهد. 45 دست دادن اتفاق می افتد.. در این مهمانی چند نفر شرکت کرده اند؟ نشان دهید که چگونه فهمیدید. توسعه 1- از دانش آموزان بخواهید که روش یافتن جمع اعداد متوالی را به صورت ...+3+2+1=2/(1+n)(n) بررسی کنند. 2- از دانش آموزان بخواهید که تعداد اقطار یک چند ضلعی را تعیین کنند. تعداد اقطار برابر است با 2/(1-n)(n). دانش آموزان باید توجه کنند که چگونه این مسئله با مسئله ی دست دادن ها مرتبط است.3- دانش آموزان مسئله ی زیر را حل کنند.در یک مدرسه، جلسه ای برگزار شد. در این جلسه 6 مدرسه شرکت داشتند که 2 معلم از هر 5 مدرسه و 2 معلم از مدرسه ی میزبان حضور داشتند. تعداد کل معلم ها 12 نفر بود. تعدادی از معلم ها همدیگر را می شناختند. همه ی معلمانی که همدیگر را نمی شناختند، با هم دست دادند. سپس یکی از معلمان مدرسه ی میزبان از همه ی معلم های دیگر پرسید که هر کدام از آن ها چه تعداد دست داده اند. هر کسی جواب متفاوتی داد. دیگر معلم مدرسه ی میزبان، با چند نفر دست داده است؟ پاسخ این مسئله با رسم نمودار به راحتی پیدا می شود. دانش آموزانی که می خواهند مسئله را با فرمول یا معادله حل کنند، به زودی متوجه می شوند که امکان پذیر نیست. بررسی اجرای طرح درس در کلاس - برخی راه هایی که دانش آموزان نشان می دهند که به طور فعال در فرایند یادگیری تعداد دست دادن ها شرکت کرده اند، چیست؟- در این درس چه سطحی از مفاهیم را جمع بندی کرده اید؟ آیا این جمع بندی مناسب بود؟- چگونه دانش آموزان را به رقابت می طلبید؟- آیا مسئله ی دست دادن ها را به تعداد اقطار چند ضلعی مرتبط کرده اید؟ اگر این طور است، این موضوع، چگونه سطح کیفی درس را افزایش داد؟- دانش آموزان چگونه فهم خود را از یک الگو، نشان می دهند؟ دانش آموزان چگونه فهم خود را از رابطه ی متغیردار نشان می دهند؟ مترجم: وحید رستمی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 571]
-
گوناگون
پربازدیدترینها