محبوبترینها
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1846049112
فراتر از دست دادن
واضح آرشیو وب فارسی:تبیان: فراتر از دست دادناهدافدانش آموزان:- رابطه ی بین مسئله ی دست دادن ها، اعداد مثلثی و جمع اعداد صحیح مثبت را خواهند فهمید. - از فرمول ها برای تعمیم الگوها در برگه ی ضمیمه استفاده و آن را رسم خواهند کرد. وسایل لازم- صفحه ی دست دادن ها- برگه ی فعالیت اعداد مثلثی- صفحه ی جمع اعداد صحیح مثبت طرح درس در این درس، دانش آموزان تعداد مثلث ها را بررسی می کنند و ارتباط آن را با مسئله ی دست دادن ها که در درس اول این بخش بررسی شد، مشاهده می کنند. ابتدا دانش آموزان مسئله ی دست دادن ها را مرور خواهند کرد. کلاس را با نمایش برنامه ی صفحه ی دست دادن ها شروع کنید و بررسی کنید که دانش آموزان برای استفاده از این صفحه به چه پیش زمینه ای نیاز دارند و از این طریق مسئله ی دست دادن ها را مرور نمایید. می توانید با انتخاب هر یک از عنوان های پایین صفحه به برگه های متفاوت در این فایل دسترسی پیدا کنید. نمودار دست دادن ها یک منحنی را نشان می دهد که تعداد افراد را با تعداد دست دادن ها مقا یسه می کند. فرمولی را که دانش آموزان برای تعداد دست دادن n نفر یا فته بودند، مرور کنید: 2/(n)(n-1). از دانش آموزان بخواهید تا فرمول را برای هر تعدادی بیان کنند. با مرور توضیحات زیر، دانش آموزان را در فهم صفحه ی دست دادن ها راهنمایی کنید:- ستون ها با استفاده از حروف (C,B,A) و سطرها با اعداد (1 و 2 و 3) مشخص می شوند.- خانه ها با توجه به حرف ستون و شماره ی سطر مشخص می شوند: D4 , C1 , B2 , A1 و غیره. به عنوان مثال، خانه ی ستون پنجم و سطر هفتم برابر است با EV. در جدول دست دادن های صفحه ی دست دادن ها، در خانه ی A3 عدد یک نوشته شده است. از دانش آموزان بپرسید: "چگونه می توانیم فرمولی بنویسیم که در A4 عدد2، در A5 عدد 3 و به همین ترتیب اعداد بقیه ی خانه ها را بدهد؟ توضیح دهید که اعداد می توانند دستی نوشته شوند. اما استفاده از فرمول، باعث می شود خانه ها را به طور نامحدود تعمیم دهیم. (این فرمول "=1+A3" باید در A4 جایگزین شود. سپس دستور Filldown از منوی ویرایش می تواند برای جایگزینی این فرمول در خانه های بعدی استفاده شود.) این فرمول را که در برخی از خانه ها نمایش داده شده، به دانش آموزان نشان دهید. آن ها باید توجه کنند که برنامه ی صفحه ی دست دادن ها، شماره ی خانه ها را به طوری که همیشه به خانه ی قبلی یکی اضافه می کند، تغییر می دهد. از دانش آموزان بپرسید که از اعداد ستون افراد چگونه استفاده کنیم تا اعداد ستون دست دادن ها را تعمیم دهیم. (با یک نفر هیچ دست دادنی وجود ندارد. بنابراین در B3 عدد صفر را بنویسید. در B4، فرمول A4*A3/2 را قرار دهید. دوباره با استفاده از دستور Filldown فرمول را در خانه های بعدی کپی کنید.) از دانش آموزان بخواهید فرمول هایی را که در خانه ها نمایان می شوند، بررسی کنند. سپس، از صفحه ی دست دادن ها برای ایجاد یک منحنی استفاده کنید. منحنی را امتحان کنید و از دانش آموزان بخواهید آن را با منحنی هایی که در خلال درس قبلی ایجاد کرده اند، مقایسه کنند. بپرسید آیا این منحنی خطی است؟" (نه، خطی نیست.) از دانش آموزان بپرسید چگونه فهمیده اند که منحنی خطی نیست. برگه ی فعالیت تعداد مثلث ها را توزیع کنید. از دانش آموزان بخواهید تا پنجمین عدد مثلثی را روی برگه هایشان رسم کنند. سپس دانش آموزان باید به صورت انفرادی، جدول برگه ی فعالیت را کامل کنند. هنگامی که دانش آموزان کار می کنند، کلاس را تحت نظر داشته باشید. وقتی بیشتر دانش آموزان جدول را کامل کردند، از آن ها بخواهید که کارشان را با هم گروهی خود به اشتراک بگذارند. سپس در مورد نتایج، بحث کنید.
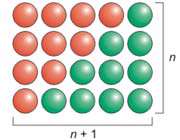
دانش آموزان باید الگوهای 1،3،6 و 10 را که در مسئله ی دست دادن ها با آن رو به رو شده بودند، تشخیص دهند. (تعداد نقطه ها برابر است با عدد شکل ضرب در عدد شکل بعدی، تقسیم بر2.) از دانش آموزان بپرسید "این الگو با مسئله ی دست دادن ها چه تفاوتی دارد؟" (ما عدد بعدی را بررسی می کنیم نه عدد قبلی را.) به دانش آموزان فرصت دهید تا یک منحنی در برگه ی فعالیت رسم کنند. از دانش آموزان بخواهید این اطلاعات را درصفحه ی دست دادن ها وارد کنند و یک منحنی در کامپیوتر ایجاد کنند. تصویری نیز برای تشریح تعداد مثلث ها (همان طور که در زیر نشان داده شده) می تواند مورد استفاده قرار گیرد. این مستطیل شامل n(n+1) نقطه می باشد. وقتی مستطیل نصف می شود، به شکل یکی از اعداد مثلثی در می آید که تعداد نقطه ها برابر است با n(n + 1) ÷ 2.
برای فراهم کردن مثال دیگری از الگوی عدد مثلثی، از دانش آموزان بخواهید که صفحه ی جمع اعداد صحیح را بررسی کنند. این صفحه، فهرست n عدد صحیح مثبت است. از دانش آموزان بپرسید: "از چه اطلاعاتی که پیش از این کسب کرده ایم، می توانیم استفاده کنیم؟" دانش آموزان جمع n عدد را به خاطر خواهند آورد، یعنی 1 + 2 + 3 + ... + n = n(n + 1) ÷ 2دانش آموزان باید بررسی کنند که آیا این منحنی خطی خواهد بود. (منحنی خطی نیست، چون آهنگ تغییر ثابت نیست. همچنین n ضرب در (n+1) جمله ای بر حسب n2 در معادله ایجاد خواهد کرد.) پرسش هایی برای دانش آموزاناعداد مثلثی چگونه به مسئله ی دست دادن ها مرتبط می شود؟ این دو مسئله چه تفاوتی با هم دارند؟(این الگو ضرب اعداد متوالی، تقسیم بر 2 است. مسئله ی دست دادن ها ضرب در عدد قبلی بود ولی در اعداد مثلثی ضرب درعدد بعدی است.)چگونه می توانید خطی یا غیر خطی بودن نموداری را بفهمید؟ از طریق جدول مقادیر چگونه می توانید بیان کنید؟ از طریق معادله چگونه می توانید بیان کنید؟ (نمودار غیر خطی، آهنگ تغییر ثابتی در جدول نخواهد داشت، اما نمودار خطی آهنگ تغییر ثابتی دارد. از طریق معادله، اگر بیشترین توان متغیر، بزرگ تر از یک باشد، نمودار غیر خطی خواهد بود.)چگونه می توان جمع n عدد صحیح مثبت متوالی را که از عدد 1 شروع می شود، به شکل فرمول نوشت؟ [n(n + 1) ÷ 2] ارزشیابیاز دانش آموزان بخواهید که صفحه ی گسترده ی خود را پرینت بگیرند. این صفحه ی گسترده ها با نمایش فرمول ها و نمودارهای آن ها، توسط آنها در استفاده از صفحه گسترده برای مدل سازی یک مسئله را نشان می دهد.از دانش آموزان بخواهید که جمع اولین 34 عدد صحیح مثبت (300) را با بیش از یک روش، نشان دهند (300=25/2×24). دانش آموزان می توانند از صفحه ی گسترده ی روش گاوس، n(n+1)/2 ، ماشین حساب، نمودار و غیره استفاده کنند توسعه1- جمع اولین n عدد فرد صحیح مثبت را بررسی کنید. برای مثال، 9=5+3+1 و بعد از آن، 16=7+5+3+1. چه معادله ای جمع اولین n عدد فرد صحیح مثبت را ارائه می دهد؟ (n2)2- اعداد هرمی را با ساختن مدلی از اولین 4 عدد مثلثی به وسیله ی توپ های پینگ پنگ، بررسی کنید. (توپ ها را به هم وصل کنید.) وقتی آن ها را به هم متصل می کنید، چه اتفاقی می افتد؟ (1، 3، 6 و 10 اعداد مثلثی هستند. اولین هرم 1 است، بعد 4، 10 و 20.) این اعداد را چه می نامند؟ (اعداد هرمی). صفحه ی سوم و چهارم برگه ی فعالیت اعداد مثلثی می تواند برای بررسی اعداد هرمی مورد استفاده قرار گیرد.3- از دانش آموزان بخواهید تا مثلث پاسکال را بررسی کنند. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 اعداد مثلثی در مثلث پاسکال، در کجا قرار دارند؟ اعداد هرمی چطور؟4- گفته می شود وقتی کارل فردریک گاوس به سرعت حاصل جمع 10+...+3+2+1 را یافت، معلم خود را متحیر کرد. او به طور فرضی می فهمد که 101=100+1 ، 101=99+2 و همینطور 50 جفت وجود دارد که جمع آنها برابر 101 است، در نتیجه جمع کل برابر است با 5050=101×50. حتی اگر این داستان حقیقت نداشته باشد، انگیزه ای برای مطالعه ی الگوهای این درس، فراهم می کند. از دانش آموزان بخواهید در مورد گاوس تحقیق کنند. او چه سهمی در ریاضیات دارد؟ بررسی اجرای طرح درس در کلاس1- آیا وقتی از صفحه ی گسترده استفاده می کنید، دانش آموزان بیشتر تشویق می شوند؟ چگونه استفاده از تکنولوژی می تواند برای این درس مفید باشد؟2- دانش آموزان چگونه ارتباط بین مسائل مختلفی را که به هم مرتبطند، پیدا می کنند؟3- شیوه ی آموزشی شنیداری، تکنیکی و بصری این درس چگونه است؟4- آیا این درس را می توان تعمیم داد؟ شما چه تغییراتی ایجاد می کنید؟ مترجم: وحید رستمی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 851]
-
گوناگون
پربازدیدترینها