محبوبترینها
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1846163380
بافتن مواردی که تغيير نمی کنند
واضح آرشیو وب فارسی:تبیان: بافتن مواردي که تغيير نمي کنند
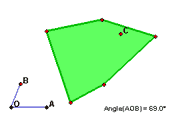
اهدافدانش آموزان قادر خواهند بود:- تأثير دوران تحت زاويه اي مشخص و يا تأثير ترکيب دو يا چند دوران را پيش بيني کنند.- زوايايي را که شکل با دوران تحت آن زوايا تغيير نمي کند، پيدا کنند. طرح درسشکل زير يک پرچم سبز به مرکز دوران C مي باشد.7. در ذهن خود پرچم را ْ90 در خلاف جهت حرکت عقربه هاي ساعت دوران دهيد و شکل آن را روي کاغذ رسم کنيد. سپس زاويه ي دوران را با حرکت دادن نقطه ي B، روي ْ90 تنظيم کنيد و روي دکمه ي "Show Rotated Figure " کليک کنيد تا نتيجه را مشاهده کنيد. آيا موقعيت پرچم با شکلي که شما رسم کرده ايد، يکسان است؟ براي ديدن محيط تعاملي، نرم افزار جاوا را از اينجا دريافت کنيد.8. روي دکمه ي "Start Over " کليک کنيد. زاويه ي ديگري انتخاب کنيد و شکلي را که فکر مي کنيد حاصل مي شود، رسم کنيد. نقطه ي B را براي تنظيم زاويه ي دلخواه خود حرکت دهيد و سپس روي دکمه ي "Show Rotated Figure" کليک کنيد تا نتيجه را مشاهده کنيد. شکل آبي رنگ را با شکلي که خودتان رسم کرده ايد، مقايسه کنيد.با جا به جا کردن نقطه ي C و نقاط پرچم، وضيت شکل را تغيير دهيد. تمرين 8 را تکرار کنيد.9. مرکز دوران را در چه مکاني مي توانيد قرار دهيد که بدون توجه به زاويه ي دوران، نقطه اي روي شکل پيدا شود که اصلا ً حرکت نکند و ثابت بماند.10. براي مرکز دوران مشخص، چه نقطه اي تحت هر دوراني ثابت باقي خواهد ماند؟ ترکيب دوران ها اگر دوران ها را پي در پي انجام دهيم، تلفيق همه ي دوران ها را ترکيب دوران ها مي گوييم.11. وقتي شکلي حول مرکز ثابتي دو بار مي چرخد، چه اتفاقي مي افتد؟12. از ترکيب دو دوران ْ90، دوران تحت چه زاويه اي به دست مي آيد؟13. نتيجه ي ترکيب دوران ْ 40 با دوران ْ60 چيست؟14. نتيجه ي ترکيب دو دوران ْ240 چيست؟15. چگونه مي توانيد يک زاويه ي بزرگ تر از ْ 360 را به يک زاويه ي کوچک تر از ْ360 تبديل کنيد؟ شکل هايي که تحت دوران ثابت مي مانند مرکز دوران هميشه تحت دوران، ثابت باقي مي ماند اما بعضي وقت ها کل شکل تحت دوران بدون تغيير باقي مي ماند.16. با دوران تحت چه زاويه اي، همه ي اشکال بدون تغيير باقي مي مانند؟17. هر يک از اشکال زير را حول نقطه ي C، تحت همه ي زوايايي که شکل قرمز را خلاف جهت حرکت عقربه هاي ساعت مي چرخاند، دوران دهيد تا شکل قرمز بر شکل سبز منطبق شود. براي ديدن محيط تعاملي، نرم افزار جاوا را از اينجا دريافت کنيد.18. با تغيير زواياي دوران، چه الگوهايي را مشاهده مي کنيد؟19. اگر مرکز دوران تغيير کند، چه اتفاقي مي افتد؟20. مرکز دوران و زواياي دوران بايد چگونه انتخاب شوند تا يک شش ضلعي منتظم تحت دوران بدون تغيير باقي بماند؟ آيا مي توانيد اين مشاهدات را تعميم دهيد؟اکنون شما مي توانيد روش توصيف تقارن اشکال را توسط رياضيدانان، بفهميد. اين موضوع در بخش بعدي درس، مورد بحث قرار مي گيرد. مترجم: وحيد رستمي
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 310]
-
گوناگون
پربازدیدترینها