تبلیغات
تبلیغات متنی
آموزشگاه آرایشگری مردانه شفیع رسالت
دکتر علی پرند فوق تخصص جراحی پلاستیک
بهترین دکتر پروتز سینه در تهران
محبوبترینها
راهنمای انتخاب شرکت‌های معتبر باربری برای حمل مایعات در ایران
چگونه اینورتر های صنعتی را عیب یابی و تعمیر کنیم؟
جاهای دیدنی قشم در شب که نباید از دست بدهید
سیگنال سهام چیست؟ مزایا و معایب استفاده از سیگنال خرید و فروش سهم
کاغذ دیواری از کجا بخرم؟ راهنمای جامع خرید کاغذ دیواری با کیفیت و قیمت مناسب
بهترین ماساژورهای برقی برای دیسک کمر در بازار ایران
بهترین ماساژورهای برقی برای دیسک کمر در بازار ایران
آفریقای جنوبی چگونه کشوری است؟
بهترین فروشگاه اینترنتی خرید کتاب زبان آلمانی: پیک زبان
با این روش ساده، فروش خود را چند برابر کنید (تست‌شده و 100٪ عملی)
خصوصیات نگین و سنگ های قیمتی از نگاه اسلام
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1866249619
کشف الگوها در قضیه ی پیک
واضح آرشیو وب فارسی:تبیان: کشف الگوها در قضیه ی پیک این درس، با استفاده از یک تخته ی میخی و یا اپلت تخته میخی، دانش آموزان می توانند الگوهای قضیه ی پیک را بیابند. اهدافپس از تکمیل این درس دانش آموزان می توانند: اشکال مختلف روی تخته ی میخی را برای تعیین رابطه ی بین تعداد نقاط محیطی، تعداد نقاط داخلی و مساحت شکل بررسی کنند. با استفاده از علامت های جبری برای نمایش این رابطه، معادله بسازند. وسایل لازمتخته ی میخی و نوار یا مدل سازی تخته میخیبرگه ی فعالیت کشف قضیه ی پیک طرح درسدر درس اول، قضیه ی پیک برای دانش آموزانی که با این قضیه آشنا نیستند، تدریس و برای دانش آموزانی که با آن آشنا هستند، یادآوری می شود. یکی از انواع تخته های میخی را در اختیار دانش آموزان قرار دهید. تخته ی میخی و نوارهای لاستیکی و یا تخته ی میخی مقوایی. اگر به رایانه دسترسی دارید، می توانید از مدل سازی تخته ی میخی نیز استفاده کنید. از دانش آموزان بخواهید با کمک نوارهای لاستیکی چند شکل بسازند. سپس توجه آن ها را به تعداد نقاط محیطی (P) و نیز تعداد نقاط داخلی (A) هر شکل جلب کنید. می توان دانش آموزان را تشویق کرد تا برای ثبت یافته های خود با این داده ها نمودار تهیه کنند.
ممکن است محاسبه ی درست مساحت شکل، در ابتدای فعالیت برای دانش آموزان دشوار باشد. پیش از این مرحله، توضیح دهید شکل را به مستطیل های کوچک تقسیم کنند. این کار به آن ها کمک می کند تا بتوانند مساحت شکل را آسان تر حساب کنند. برای مثال برای تعیین مساحت مثلث زیر، می توان ابتدا مساحت مربع محیط بر آن را محاسبه و سپس مساحت قسمت های اضافی را از آن کم کرد.
مساحت این مربع، 4 واحد مربع است و مساحت کل قسمت های اضافی 2.5 واحد مربع است. در نتیجه مساحت مثلث 1.5=2.5-4 واحد مربع است. برگه ی فعالیت کشف قضیه ی پیک را بین دانش آموزان پخش کنید و به دانش آموزان کمک کنید تا بررسی خود را شروع کنند. پرسش های 1 تا 5، پرسش های اساسی و پایه ای این فعالیت است و در پرسش های 6 تا 14، به دانش آموزان کمک می شود تا گام به گام این فعالیت را انجام دهند. (می توان برگه های فعالیت را یکی یکی به شاگردان داد و برگه های بعدی را پس از انجام مراحل قبلی بین آن ها توزیع کرد.)
برگه ی فعالیت کشف قضیه ی پیکبرگه ی فعالیت کشف قضیه پیک:این برگه، طوری طراحی شده است تا دانش آموزان به طور مداوم با فرضیات شخصی و فرموله کردن این فرضیات در گروه خود، مشغول باشند. با گروه بندی دانش آموزان، اعضای گروه نتایج محاسبات هم گروهی های خود را کنترل می کنند. در پایان این فعالیت، دانش آموزان باید به فرمول زیر در قضیه ی پیک، برسند. A = 1/2 P + I – 1 همچنین می توانید فعالیت پژوهشی در مفهوم مثلث و خواص چند ضلعی ها: ساخت چند ضلعی ها را با دانش آموزان انجام دهید.پرسش هایی برای دانش آموزچگونه می توان مساحت شکل های نامنظم را محاسبه کرد؟[یکی از روش های محاسبه ی مساحت اشکال نامنظم، استفاده از قضیه ی پیک است؛ البته با این فرض که می توان این اشکال را طوری بر روی صفحه ی مختصات قرار داد که رئوس شکل بر نقطه های مختصاتی منطبق شوند.] مساحت اشکال مختلف در صورت داشتن تعداد نقاط محیطی متفاوت و تعداد نقاط داخلی یکسان چه رابطه ی با هم دارند؟ تغییر تعداد نقاط محیطی چه ت?ثیری دارد؟ [وقتی تعداد نقاط محیطی 1 واحد افزایش می یابد، مساحت به اندازه 2/1 تعداد نقاط محیطی زیاد می شود.]مساحت اشکال مختلف در صورت داشتن تعداد نقاط داخلی متفاوت و تعداد نقاط محیطی یکسان چه رابطه ی با هم دارند؟ تغییر تعداد نقاط داخلی چه ت?ثیری دارد؟ [وقتی تعداد نقاط داخلی 1 واحد افزایش می یابد، مساحت به اندازه ی 1 واحد زیاد می شود.] ارزشیابیمی توان از دانش آموزان خواست تا ارزیابی خود را درباره ی فرایند کشف، توانایی تولید اشکال با تعداد میخ های محیطی و داخلی بنویسند و مشخص کنند بحث های گروهی چه مقدار به پدیدار شدن سریع تر معادله کمک می کند. توسعه1- اگر فرصت هایی برای دانش آموزان ایجاد کنید که با P و A معلوم، اشکال ابتکاری بسازند، از این کار لذت می برند. برای مثال، از آن ها بخواهید تا اشکالی بسازند که 9 نقطه ی محیطی و 3 نقطه ی داخلی دارد. (برخی از اشکال ممکن، در زیر آورده شده است.)
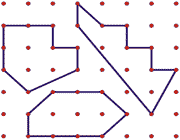
2- برای ایجاد معادله، از دانش آموزان بخواهید تا مساحت اشکال را با استفاده از چند مکعب بیابند. (چون ممکن است در مساحت بعضی از اجسام 2/1 وارد شود، از آن ها بخواهید تا دو مکعب را به عنوان واحد مساحت استفاده کنند.) از آن ها بخواهید تا این مکعب را طوری روی محورهای مختصات قرار دهند که P روی محور x و I بر روی محور y باشد. بنابراین شکلی با مساحت 6.5 باید در نقطه ی (3، 9) باشد. با این نمودار دانش آموزان می توانند ببینند با ثابت نگه داشتن P یا I مساحت شکل چه تغییری می کند. 3- از دانش آموزان بخواهید تا به کمک یک برگه ی نقطه چین، مساحت اشکال نامنظم را تخمین بزنند. از آن ها بخواهید اشکالی را که خود رسم می کنند، بررسی کنند. چند شکل در حالت های خاص نیز خودتان برای آن ها ترسیم کنید. بررسی اجرای طرح درس در کلاسآیا از برگه ی فعالیتی استفاده کردید؟ آیا برگه ی فعالیتی ساختارهای زیادی را مهیا می کند؟ ترجیح می دهید در جلسات آموزشی بعدی، تنها از نصف ساختارهای موجود در برگه ی فعالیتی استفاده کنید؟ آیا در محاسبه ی مساحت اشکال با تعداد اضلاع فرد، دانش آموزان به راهنمایی های بیشتری نیاز دارند؟ آیا در جلسه های آموزشی بعدی برای اجرای این روش، ابتدا تعیین مساحت مثلث را یادآوری می کنید؟آیا برای تحقق اهداف این درس، طرح درس را تغییر دادید و اصلاحاتی در آن انجام دادید؟ اگر این کار را کردید برای این که دانش آموزان درس را بفهمند، چه فعالیت دیگری پیشنهاد می کنید؟ مترجم: راضیه کریمی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 2272]
-
گوناگون
پربازدیدترینها