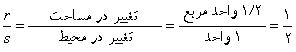تبلیغات
تبلیغات متنی
محبوبترینها
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
پروازهای مشهد به دبی چه زمانی ارزان می‌شوند؟
تجربه غذاهای فرانسوی در قلب پاریس بهترین رستوران‌ها و کافه‌ها
دلایل زنگ زدن فلزات و روش های جلوگیری از آن
خرید بلیط چارتر هواپیمایی ماهان _ ماهان گشت
سیگنال در ترید چیست؟ بررسی انواع سیگنال در ترید
بهترین هدیه تولد برای متولدین زمستان: هدیه‌های کاربردی برای روزهای سرد
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1833367118
آهنگ تغییر در قضيه ی پيک
واضح آرشیو وب فارسی:تبیان: آهنگ تغيير در قضيه ي پيکدانش آموزان از صفحه ي گسترده براي بررسي آهنگ تغيير در ميان اشکال مختلف ايجاد شده بر روي تخته ي ميخي استفاده مي کنند. به کمک آهنگ تغيير، به راحتي مي توان ضريب قضيه ي پيک را پيدا کرد. اهدافپس از اتمام اين درس دانش آموزان مي توانند: صفحه ي گسترده اي براي بررسي قضيه ي پيک ايجاد کنند. با تغيير مقادير سطر و ستون به دنبال تفاوت مساحت ها بوده و با کمک آن درباره ي آهنگ تغيير بحث کنند. وسايل لازمتخته ي ميخي و نوار لاستيکي (يا وسيله ي ديگري)صفحه ي گسترده ي قضيه ي پيکرايانه با برنامه ي صفحه گسترده (اختياري) هدف اين درس، کاربرد صفحه ي گسترده به عنوان ابزار مشاهده ي الگوها در چندين خانه ي جدول است. از آن جا که مساحت به دو متغير يعني تعداد نقاط داخلي و محيطي وابسته است، استفاده از شيوه ي ارائه صفحه ي گسترده، طبيعي است. وقتي از تخته ي ميخي فيزيکي استفاده مي کنيد، دانش آموزان به طور طبيعي بر روي نقاط محيطي متمرکز مي شوند، زيرا افزايش مقادير نقاط محيطي آسان تر از افزايش نقاط داخلي است. وقتي از صفحه ي گسترده استفاده مي کنيد، دانش آموزان ابتدا تأثير نقاط داخلي را مشاهده مي کنند. کلاس را گروه بندي کنيد و از هر گروه بخواهيد صفحه ي گسترده اي ايجاد کرده و مقادير نقاط محيطي را در سطر اول و مقادير نقاط داخلي را در ستون اول درج کنند. وقتي دانش آموزان مي فهمند با مقدار 0، 1و 2 براي نقاط داخلي، هيچ شکلي نمي توانند بسازند، بحث گرمي بين آن ها ايجاد مي شود. بعد از آن، مي فهمند که مقادير نقاط داخلي را بايد از 3 شروع کرد. اما شکل هاي مختلفي با مقدار صفر براي نقاط داخلي مي توان ساخت. بنابراين مقادير نقاط داخلي از صفر شروع مي شود. دانش آموزان مي توانند با استفاده از برنامه ي اکسل، Quattro يا ديگر برنامه هاي کاربردي براي ايجاد صفحه ي گسترده بر روي رايانه، صفحه ي گسترده اي بسازند يا اين که از برگه ي فعاليت صفحه ي گسترده ي پيک استفاده کنند. (با استفاده از برنامه ي ايجاد صفحه ي گسترده در رايانه، دانش آموزان پس از تعيين الگو، مي توانند باقي ستون ها را به طور خودکار پر کنند.)
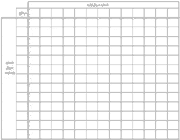
ممکن است گروه ها بخواهند خانه هاي جدول را به طور نامنظم پر کنند يا آن که به صورت منظم و به ترتيب، ابتدا سطرها و سپس ستون ها را پر کنند. البته با استفاده از روش منظم، زودتر مي توان به فرضيه ي آهنگ ثابت تغيير رسيد. در شکل زير نتايج به صورت منظم و مرتب نشان داده شده است. پس از اين که دانش آموزان حدس زدند که افزايش مقادير خانه هاي هر سطر به اندازه ي 2/1 واحد و مقادير خانه هاي هر ستون به اندازه ي 1 واحد است، از آن ها بخواهيد تا عددي را وارد جدول کنند و ببينند آيا مساحت شکلي با اين اندازه ها، برابر با مقدار پيش بيني شده است يا نه. براي مثال، ممکن است يکي از دانش آموزان با توجه به الگو، حدس بزند که مساحت شکلي با 11 نقطه ي محيطي و 9 نقطه ي داخلي 2/1 13 واحد سطح است. اعضاي گروه بايد چنين شکلي را يافته و درستي يا نادرستي حدس دوست خود را ثابت کنند.
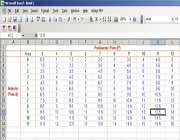
پس از آن که دانش آموزان با موفقيت الگو را تمرين کردند، از همه بخواهيد تا در مورد آهنگ تغيير بحث کنند. سپس از گروه ها بخواهيد تا با علايم جبري، براي الگوي خود، فرمولي به دست بياورند. اگر دانش آموزان، درس هاي قبلي اين مجموعه يعني قضيه ي پيک به عنوان يک دستگاه معادلات و کشف الگوي قضيه ي پيک را مطالعه نکرده باشند، يافتن اين فرمول برايشان دشوار خواهد بود. اما اگر اين دروس را مطالعه کرده باشند، به سرعت مي توانند اين فرمول را به دست آورند. توجه به ضريب P مي تواند بحث داغي بين دانش آموزان ايجاد کند. با توجه به اين که اين ضريب، آهنگ تغيير را نشان مي دهد مي توان آن را به صورت r/s نشان داد که r تغيير در مساحت و s تغيير در تعداد نقاط محيطي است. بنابراين، هر وقت تعداد نقاط محيطي به اندازه ي 1 واحد زياد مي شود، ضريب P نشان دهنده ي 2/1 واحد مربع تغيير در مساحت است. يعني:
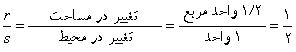
به همين ترتيب هر بار که تعداد نقاط داخلي به اندازه ي 1 واحد زياد مي شود، مساحت به اندازه ي 1 واحد مربع افزايش مي يابد. پس ضريب P يک است. با اين حساب فرمول به صورت زير است: A = 1/2 P + 1 I . دانش آموزان با توجه به الگوها مي فهمند که مساحت هر شکل 1 واحد کم تر از مقداري است که با فرمول محاسبه مي شود. پس شکل صحيح فرمول به شکل زير است: A = 1/2 P + I - 1در کلاس جبر يا حسابان، ساخت فرمول و بحث درباره ي شيب، نقطه ي توقف خوبي است. در کلاس حسابان که فضا براي تشريح مفهوم مشتق جزيي آماده است، پرسش هاي زير را مطرح کنيد: "مفهوم اين که يک متغير را ثابت نگه مي داريم و متغير ديگر را تغيير مي دهيم، چيست؟" محاسبه ي مشتق جزيي، بخشي از معرفي و توضيح موضوع است. معادله ي A = 1/2 P + I – 1 داده شده است. اگر I ثابت نگه داشته شود، مشتق جزئي A نسبت به P، برابر با 2/1 مي شود. اين نتيجه، همان پديده اي است که دانش آموزان در صفحه ي گسترده به آن مي رسند. به همين روش اگر P ثابت نگه داشته شود، مشتق جزيي A نسبت به I، برابر با 1 مي شود. البته چون قضيه ي پيک پيوسته نيست، نمي توان از آن مشتق جزئي گرفت. اما مثال و بحث در مورد ثابت نگه داشتن يک متغير در حالي که متغير ديگر مي تواند تغيير کند، م?ثر است. اين موضوع را مي توان براي ايجاد بحث داغي درباره ي پيوستگي به کار برد. پرسش هايي براي دانش آموزچه مقاديري براي P قابل قبول است؟ چه مقاديري براي I قابل قبول است؟[هيچ شکلي را نمي توان با کم تر از سه نقطه ي محيطي درست کرد. بنابراين مقادير 0، 1 و 2 براي P قابل قبول نيست. از سوي ديگر، با هر تعداد نقاط داخلي، مي توان شکلي ساخت. بنابراين همه ي مقادير صحيح براي I قابل قبول است.]بهترين روش براي پر کردن صفحه ي گسترده چيست؟[با توجه به اين که تعداد الگوها در اين جا محدود است، تکميل سطرها و ستون هاي اين جدول آسان است. دانش آموزان بايد توجه کنند که مقادير به اندازه ي 2/1 از يک ستون به ستون بعدي و به اندازه ي 1 از هر سطر به سطر بعدي افزايش مي يابد. با اين اطلاعات تکميل صفحه ي گسترده آسان تر مي شود.] آهنگ تغيير در معادله ي رياضي چگونه است؟ [ضريب 2/1 در جلوي P، نشان مي دهد که با افزايش تعداد نقاط داخلي به اندازه ي 1 واحد، مساحت به اندازه 2/1 در تعداد نقاط داخلي افزايش مي يابد. به همين ترتيب، ضريب 1 در جلوي I نشان مي دهد که با افزايش تعداد نقاط محيطي به اندازه ي 1 واحد، مساحت به اندازه ي 1 واحد مربع افزايش مي يابد.] ارزشيابي1-از دانش آموزان بخواهيد تا نامه اي به دوست غايب خود بنويسند و ضمن راهنمايي براي انجام اين فعاليت، مفاهيم کليدي و روش هاي جلوگيري از اشتباه را براي وي توضيح دهند. از آن ها بخواهيد تا مطالب را با ادبياتي بنويسند که هم کلاسي شان درس را بفهمد و در صورت لزوم مي توانند از مثال استفاده کنند. 2-پرسش هايي مطرح کنيد که دانش آموزان مجبور شوند براي حل آن، به جاي فرمول نهايي از آهنگ تغيير استفاده کنند. براي مثال "فرض کنيد مساحت شکلي 2/1 4 است. اگر شکل ديگري با همان تعداد نقاط محيطي و با تعداد نقاط داخلي که 1 واحد از تعداد نقاط محيطي آن بيشتر است، بسازيم، مساحت آن چه قدر مي شود؟" دانش آموزان را تشويق کنيد تا بدون مراجعه به صفحه ي گسترده به اين پرسش پاسخ دهند. پس از آن بپرسيد: "مساحت شکلي با 10 نقطه ي داخلي بيشتر چقدر است؟ " سپس امتحاني کوتاه با پرسشي درباره ي کاربرد آهنگ تغيير براي نقاط محيطي بگيريد و از آن ها بخواهيد تا راه حل مسئله را کامل بنويسند. توسعه1-ممکن است دانش آموزان بخواهند بعضي از ستون يا سطرهاي جدول را رنگي کنند تا بعضي از الگوها را متمايز کنند. از اين کار مي توان براي ترسيم نمودار معادله با دو متغير مستقل استفاده کرد. از دانش آموزان بخواهيد تا از مکعب ها براي ايجاد ارتفاع در خانه هاي جدول صفحه ي گسترده استفاده کنند. اين کار، درک مفهوم سرعت تغيير را با تغيير سطرها و ستون ها تقويت مي کند. 2-از دانش آموزان بپرسيد: "چه کسي مي تواند اين فعاليت را طوري کامل کند که آهنگ تغيير در خطي مانند y = 3x – 5 يا y = -3/4 x + 1 را نشان دهد؟" اين کار کمک مي کند تا درک دانش آموزان از مفهوم آهنگ تغيير تقويت شده و دانش آموزان ميان اين مفاهيم و مفاهيم پيشين ارتباط برقرار کنند. بررسي اجراي طرح درس در کلاسآيا فناوري آموزشي صفحه ي گسترده نيازهاي آموزشي را به صورت کامل برطرف مي کند؟ آيا دوباره از اين فناوري استفاده مي کنيد يا اين فعاليت را بر روي کاغذ انجام مي دهيد؟آيا دانش آموزان جدول را به صورت نامنظم پر کردند؟ آيا اين کار مفيد است يا بايد آن ها را به سمت رهيافت منظم تري هدايت کرد؟چگونه انتقال الگوي صفحه ي گسترده به معادله ي رياضي، کار را ساده تر مي کند؟دانش آموزان در بحث آهنگ تغيير با چه مشکلاتي مواجه شدند؟ چگونه مي توان به آن ها کمک کرد تا بيشتر درگير بحث شوند؟ مترجم:راضيه کريمي
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 1375]
-
گوناگون
پربازدیدترینها