محبوبترینها
قیمت دیگ بخار و تولیدکننده اصلی دیگ بخار
معروف‌ترین هدیه و سوغاتی یزد مشخص شد!
آشنایی با انواع دوربین مداربسته ضد آب
پرداخت اینترنتی قبوض ساختمان (پرداخت قبض گاز، برق و آب)
بهترین دوره آموزش سئو محتوا در سال 1403 با نام طوفان ۱۴۰۳ در فروردین ماه شروع می شود
یک صرافی ارز دیجیتال چه امکاناتی باید داشته باشد؟
تعمیرگاه مجاز تعمیر ماشین لباسشویی در شرق تهران
تعمیرگاه مجاز تعمیر ماشین لباسشویی در شرق تهران
جراحی و درمان ریشه دندان عفونی با خانم دکتر صفوراامامی
چه مواردی بر قیمت کابین دوش حمام تاثیر دارند؟
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1798090532
الگوها و توابع
واضح آرشیو وب فارسی:تبیان: الگوها و توابع
در این درس، دانش آموزان به بررسی محیط، مساحت و حجم مربوط به شکل های هندسی دو بعدی و سه بعدی خواهند پرداخت. اهدافدانش آموزان خواهند توانست محیط، مساحت و حجم شکل های هندسی را محاسبه کنند. وسایل لازمکاشی های مربع شکل ( از مقوا )یک برگ کاغذ شطرنجی برای هر یک از دانش آموزانبرگه ی فعالیت میزها در جشن تولد طرح درسمقدمه:در یک برداشت کلی، مشاهده و دریافت الگوهای ریاضی از دانش نسبت به رشته های بسیار دیگری مانند علوم تجربی، تاریخ، اقتصاد و علوم اجتماعی برمی خیزد. مطالعه ی الگوها در ریاضیات بسیار بنیادی است. ریاضی دانان الگوها را مشاهده می کنند، آن ها درباره ی الگوها فرضیه می سازند، فرضیه ها را آزمایش می کنند، به بحث می گذارند، بیان می کنند و تعمیم می دهند. در روند این مراحل، آن ها مهم ترین ویژگی های الگو را " کشف می کنند"، برداشت هایی از مفاهیم و روابط به وجود می آورند، زبانی برای صحبت کردن درباره ی الگوها ایجاد می کنند، آن ها را با هم تلفیق می کنند و بین آن الگو و الگوهای دیگر تمایز قائل می شوند. هنگامی که روابط بین کمیت های یک الگو را بررسی می کنیم، دانشی درباره ی روابط مهم ریاضی و توابع شکل می گیرد. کنکاش در الگوها به دانش آموزان امکان می دهد که: به حل مسائل بپردازند. درک خود را از مفاهیم پایه ای و روابط مهم ریاضی گسترش دهند. روابط بین کمیت ها ( متغیرها ) را در یک الگو بررسی کنند. با استفاده از زبان متغیرها، الگوها را تعمیم دهند. الگوها را تلفیق کنند یا گسترش دهند. درک مفهوم تابع را پایه ریزی کنند. استفاده از این روش - به کارگیری الگوها برای تحقیق در حل مسائل - به دانش آموزان امکان می دهد تا به قبل و بعد مسئله بیندیشند، الگوها را ببینند، تعمیم دهند، گسترش دهند، تلفیق کنند و ارزشیابی کنند. در چنین روشی، دانش آموز معانی و روابطی را که در ماورای پاسخ مسئله ی اصلی وجود دارد، کشف می کند. استفاده از الگوها، ابزاری است برای آموزگار تا بحث های گوناگون ریاضی را آموزش دهد. کاوش هایی که در ادامه می آیند، به دانش آموزان کمک می کنند تا درک ریاضی خود را افزایش دهند، برای فعالیت های خود استدلال داشته باشند، دریافت های خود را با یکدیگر در میان بگذارند و ارتباط هایی با سایر سرفصل های ریاضی برقرار کنند. در دوره ی راهنمایی، برنامه ریزی آموزش ریاضیات بر پایه ی تجربیات آن ها در دوره های قبلی می باشد. در دوره ی دبستان، تجربیات دانش آموزان باید شامل تشخیص دادن و گسترش الگوها، تجزیه و تحلیل، توضیح و بیان الگوها و خلق الگوها باشد. مثلاً وقتی الگویی را در اختیار دانش آموزان قرار می دهیم، باید از شاگردان دبستانی بخواهیم تا آن را ادامه دهند، درباره ی ویژگی های آن بحث کنند یا از یک موقعیت ساده، یک الگو به وجود بیاورند. در پایه های اول و دوم راهنمایی، زیر بنای محکمی در الگویابی ایجاد می کند که برای حل مسائل در دوره ی راهنمایی به کار خواهد رفت. بنابراین دانش آموزان در دوره ی راهنمایی به آزمایش الگوها و توابعی خواهند پرداخت که به آنان امکان می دهد تا مسئله ها را با روش های گوناگون بازنگری کنند و بتوانند چنین بازنگری هایی را به صورت مسئله، داستان، اجزای به هم پیوسته، تصویر، نمودار، جدول، بیان شفاهی و نماد ترجمه کنند. علاوه بر این، این آزمایش ها برای دانش آموزان امکان تجزیه و تحلیل، فرضیه سازی، تعمیم، گسترش، نقض کردن، ارزشیابی و تأمل کردن را به وجود می آورد. تجربه اول: محیط و مساحت مسأله: حداکثر مساحتنسرین کار تابستانی خود را که برگزاری مراسم جشن تولد برای کودکان است، آغاز کرده است. همسایه های او موافقت کردند که میزهای مربع شکلی را برای رفع خستگی بچه ها به او امانت بدهند. البته وقتی که بعضی از همسایه های او به سفر می رفتند، او نمی توانست از میزهای آن ها استفاده کند. بنابراین استفاده از حداقل تعداد میز برای او اهمیت داشت. او ناچار بود میزها را در کنار هم و به صورت مستطیل بچیند، زیرا همه ی بچه ها دوست داشتند در کنار هم بنشینند. در هر ضلع یک میز، تنها یک کودک می تواند بنشیند. اگر میهمانان او 18 کودک باشند، او باید چند عدد میز امانت بگیرد؟ یادداشت معلم:برای دانش آموزان کوچک تر، با استفاده از کاشی ها یک میز میهمانی 1×2 را نمایش دهید ( با استفاده از پروژکتور ) و بپرسید: " چند نفر می توانند دور این میز بنشینند؟ " (6 نفر) برای دانش آموزان بزرگتر می توانید مسأله را این گونه مطرح کنید: " مساحت مستطیلی با محیط 18 واحد، چقدر است؟ " به گروه های کوچک دانش آموزان فرصت دهید تا با استفاده از کاشی هایشان روی مسأله کار کنند و پاسخ های احتمالی را کاوش کنند. این پرسش ها را مطرح کنید: در کدام مستطیل ها کم ترین تعداد کاشی مربعی استفاده شده است؟ (1×9 یا 9×1 )کدام یک بیشترین تعداد کاشی را لازم داشت؟ ( 4×5) یا (5×4) نسرین چند عدد میز نیاز دارد؟ ( حداقل 9 عدد )داستان میزها و بچه هایی که دور میزها می نشینند، مثال خوبی برای پیوستن دنیای واقعی دانش آموزان به دنیای ریاضیات است. در این مثال، میزها نمایان گر مساحت و افراد نمایان گر محیط هستند. در توضیح ابعاد مستطیل، ضلع پایینی و کناری را به عنوان طول و عرض مستطیل معرفی کنید. تمام مستطیل هایی را که محیط 18 واحدی دارند، در جدولی مرتب کنید.
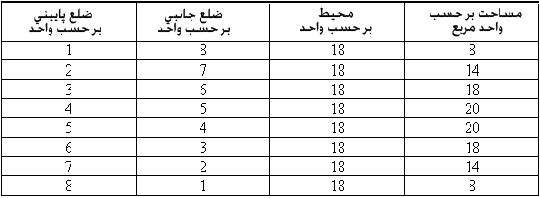
شکل 1 از دانش آموزان بخواهید تا الگوهای موجود در جدول را بیابند. هر چه طول مستطیل افزایش پیدا می کند، عرض آن کاهش می یابد و نیز هر چه طول زیاد می شود، مساحت نیز تا یک نقطه ی معین زیاد می شود و از آن نقطه به بعد شروع به کم شدن می کند. الگوی بعدی، یک توضیح شفاهی است درباره نموداری که " سهمی " یا " شلجمی " نام دارد. این موضوع باعث درک تأثیر تغییرات یک متغیر ( به نام طول ) روی متغیرهای دیگر مانند عرض و مساحت می شود. اگر اجازه داشته باشیم طول را از میان اعداد حقیقی انتخاب کنیم، آیا مستطیلی با محیط 18 واحد وجود دارد که مساحتی بزرگ تر داشته باشد؟ به احتمال زیاد دانش آموزان مستطیلی به طول 4.5 واحد را آزمایش خواهند کرد. مساحت آن 20.25 واحد است. مستطیل هایی را که طولشان بزرگ تر یا کوچک تر از 4.5 باشد، امتحان کنید. با طول های 4.4 یا 4.6 یا 4.55 واحد، مساحت هایی کمتر از 20.25 به دست خواهد آمد. مستطیلی با محیط 18 واحد، که بیشترین مساحت را دارد، شبیه مربع است که نزدیک ترین شکل به آن، مستطیل 5×4 است. نمودارهای مختلفی را می توان برای نمایش دادن اطلاعاتی که در جدول شکل 1 آمده است، رسم کرد. نمودار مساحت و ضلع پایینی ( یا ضلع جانبی ) یک سهمی است که یک تابع درجه دوم است ( شکل 2 ). نمودار ضلع پایینی و ضلع جانبی یک نمودار خطی است ( شکل 3 ).
با توجه به نمودار، از دانش آموزان بپرسید که بین دو نقطه (5و4) و (4و5) چه اتفاقی می افتد؟ در این بازه نقطه ی ماکزیمم (بیشینه) نمودار قرار دارد که با در نظر گرفتن اعداد حقیقی مقدار بیشینه را به وضوح مشاهده خواهیم کرد. از آن ها بپرسید " اندازه های مستطیلی که مساحت آن 16 واحد مربع است، چیست؟ " ( 2.5 × 6.5 ) " مساحت مستطیلی که طول آن 5.5 واحد است چقدر است؟ " ( 19.25 واحد مربع ) این نمودار، تأثیر افزایش طول را بر مساحت مستطیل به صورت عینی نمایش می دهد. بپرسید: " اگر اجازه داشته باشیم محور افقی نمودار را ادامه دهیم، چه اتفاقی می افتد؟ "" آیا می توان مستطیلی با طول 9 واحد داشت؟ " " مساحت آن چقدر است؟ " ارزشیابیمثال 1برای ارزیابی میزان درک دانش آموزان از مفهوم " حداکثر مساحت "، می توانید از آن ها بخواهید تا مراحل کار خود را برای پیدا کردن مستطیل هایی با بیشترین مساحت و محیط معین بنویسیند. این پرسش بچه ها را به فعالیت در کلاس و شرکت در بحث هایی که در کلاس جریان دارد، وا می دارد و کمک می کند تا دانش آموزان و نیز آموزگارشان میزان دریافت آن ها را از موضوع درس بفهمند. مثال 2محیط همه ی مستطیل هایی را که مساحت آن ها 72 واحد مربع است ( و عدد صحیح هم هستند ) پیدا کنید. جدولی رسم کنید و داده های خود را روی نمودار بیاورید و با استفاده از جدول و یا نمودار خود به این پرسش ها پاسخ دهید: 1-کدام مستطیل کوچک ترین محیط را دارد؟ کدام یک محیطش از همه بزرگ تر است؟ 2-اگر اجاز داشته باشیم اندازه ها را از بین اعداد حقیقی ( کسری ) هم انتخاب کنیم، محیط کدام مستطیل از همه کوچک تر و محیط کدام از همه بزرگ تر است؟ تحقیق1- پیشگویی بزرگ ترین مساحتپیشگویی کنید که با یک محیط معین و ثابت، کدام مستطیل بزرگ ترین مساحت را خواهد داشت؟ از دانش آموزان بخواهید تا پیش بینی کنند که به نظر آن ها چه موقع مساحت تغییر جهت می دهد؟ مساحت وقتی به بالاترین میزان خود می رسد که شکل آن تا حد ممکن به یک مربع نزدیک می شود. اگر از اعداد حقیقی استفاده کنیم، مستطیلی که بیشترین مساحت را دارد، یک مربع است. درستی این فرض را با محیط 20 واحد و 24 واحد آزمایش کنید. از دانش آموزان بخواهید تا حدس بزنند که چه موقع مساحت شروع به کم شدن خواهد کرد و سپس همه مستطیل هایی را که طولشان یک عدد صحیح است و محیط داده شده را دارند، پیدا کنند. برای مستطیل هایی که محیط شان 20 واحد است، ممکن است لازم باشد دانش آموزان همه ی زوج های عدد صحیح را که جمعشان "ده" است، فهرست کنند و توجه کنند. که زوج ( 5 و 5 ) نقطه ی اوج مساحت و جایی است که مساحت روند حرکتش تغییر می کند. بنابراین مربع با طول ضلع 5 واحد و مساحت 25 واحد مربع، همان مستطیلی است که با محیط ثابت 20 واحد، بزرگ ترین مساحت را دارد. برای محیط 24 واحدی، باز هم مستطیلی که بیشترین مساحت را دارد یک مربع است، با طول ضلع 6 واحد و مساحت 36 واحد مربع. برای محیط 34 واحدی، کدام مستطیل بزرگ ترین مساحت را دارد؟ اگر ابعاد آن را از اعداد صحیح انتخاب کنیم، مستطیلی با ابعاد 9×8 واحد بزرگ ترین مساحت را خواهد داشت و اگر اعداد حقیقی را هم در نظر بگیریم، مربعی به ضلع 8.5 واحد، حداکثر مساحت را خواهد داشت. 2- تعمیم دادن مراحل پیدا کردن بزرگ ترین مساحتالگویی برای یافتن مساحت یک مستطیل با محیط ثابت و معین را به دست آورید. از دانش آموزان بخواهید که توضیح دهند چگونه مستطیل های مورد نظر را پیدا کرده اند. به آن ها فرصت دهید تا درباره ی مراحل این کار بحث کنند و بعد این مراحل را به زبان نمادها ترجمه کنند. همه ی زوج های عدد صحیح را که مجموع آن ها نصف محیط است، پیدا کنید که تقریباً با هم برابر باشند. این مستطیلی است که حداکثر مساحت را دارد. برای اعداد حقیقی، از آن جا که می دانیم مستطیل دارای حداکثر مساحت ( با یک محیط معین ) یک مربع است، عددی را که یک چهارم محیط است به عنوان طول ضلع مربع در نظر بگیرید. برای دانش آموزان کوچک تر، یک توضیح شفاهی می تواند مفید باشد. این مجموعه تساوی ها نیز می توانند مورد استفاده قرار گیرند:
نگاهی به جبر: تساوی که مساحت یک مستطیل را با محیط معین توصیف می کند، یک معادله ی درجه دوم است که پیش از این با جزئیات بیشتر در جبر آموخته اند. شکل نمودار مربوط به معادله های درجه دو همیشه مانند تصویر 2 است که سهمی نام دارد. فقط این که در بعضی از آن ها شکل سهمی رو به پایان است و نقطه ی ماکزیمم دارد و در برخی دیگر سهمی رو به بالا است و نقطه ی مینیمم دارد. نقطه ی مینیمم و ماکزیمم را از روش های جبری نیز می توانیم پیدا کنیم. از دانش آموزان بخواهید تا به تقارن سهمی و این که چگونه با زوج های مربوط به ابعاد مستطیل ها ارتباط دارد، توجه کنند. مثلاً مستطیل های 4×5 و 5×4 مساحت یکسانی دارند و روی یک خط افقی قرار می گیرند. خط عمودی که از نقطه ی ماکزیمم بر محور افقی عمود می شود، محور تقارن نمودار است. این مسأله باعث به وجود آمدن درکی درباره ی برخی مفاهیم بسیار مهم از جبر و حساب می شود. از نظر هندسی، نقطه های ماکزیمم و مینیمم در نمودار نقاطی هستند که خط مماس بر نمودار در آن نقاط یک خط افقی است یبه بیان دیگر شیب آن صفر است. دانش آموزان در حین این که مشغول تعمیم دادن آن چه مشاهده کرده و مورد بحث قرار داده اند هستند، با یک روش بسیار طبیعی به مفهوم " متغییر " نیز پی برده اند. 3- مساحت ثابتاگر ما 24 عدد میز مربع شکل در اختیار داشتیم، چند نفر می توانستند دور میزها بنشینند؟ یا، محیط یک میز مستطیل شکل که مساحت کل آن 24 واحد مربع باشد، چقدر است؟ به دانش آموزان اجازه دهید تا با استفاده از کاشی های مربع شکل که در اختیار دارند، شکل میزها را بچینند و بعد فهرست همه ی مستطیل هایی را که مساحت آن ها 24 واحد مربع است، در جدولی بنویسند. اگر دانش آموزان آمادگی دارند از اصطلاحات طول و عرض استفاده کنید. هم چنین می توانید کلمات ضلع پایینی و جانبی را به کار ببرید و تأکید کنید که ما سعی می کنیم تمام مستطیل های ممکن را پیدا کنیم. پس از این که دانش آموزان مسأله را بررسی کردند، داده های به دست آمده را در جدولی مرتب کنید:
تصویر 5از دانش آموزان بخواهید که الگوهای موجود را ببینند. آیا این الگوها شبیه به الگوهای مسأله ی مربوط به " محیط ثابت " هستند؟ با افزایش طول مستطیل، عرض آن کاهش می یابد، اما محیط به تدریج کم می شود تا به یک نقطه معین می رسد و پس از آن افزایش می یابد. ولی افزایش و کاهش آن مانند مسأله ی " محیط ثابت " متقارن نیست. این موضوع را می توان با رسم نمودار آن مشاهده کرد. ( تصویر 6) حداکثر محیط، 50 واحد است که متعلق به یک مستطیل دراز و باریک به ابعاد 24×1 است و حداقل محیط، 20 واحد است متعلق به مستطیل چاق و " تقریباً مربع شکل " به ابعاد 6×4 .از دانش آموزان بپرسید که آیا می توانیم محیط بزرگ تری هم داشته باشیم؟ دانش آموزان ممکن است پیشنهاد کنند که میزها را از وسط نصف کنیم تا بتوانیم مستطیلی به ابعاد یک دوم × چهل و هشت بسازیم. بعضی دیگر از آن ها ممکن است ادعا کنند که اگر اجازه داشته باشیم از اعداد گویا ( یا حقیقی ) هم استفاده کنیم، می توانیم تا بی نهایت ادامه دهیم. درباره کوچکترین محیط چه می توان گفت؟ آیا می توانیم محیط کوچکتری هم داشته باشیم؟ ( بله، اگر طول هایی بین 4 و 6 واحد را آزمایش کنیم. ) یک ضلع را 5 واحد در نظر بگیرید، بنابراین ضلع دیگر باید 5/24 باشد. ( مساحت مستطیل 24 واحد مربع و ثابت است. ) محیط آن 6/19 واحد خواهد بود که از 20 واحد کمتر است. این روند را می توانیم تا جایی ادامه دهیم که به عددی برسیم که مربع آن عدد 24 باشد. اگر دانش آموزان شما مفهوم جذر را می دانند، می توانند با استفاده از یک ماشین حساب جذر 24 را پیدا کنند آیا می توانند جذر 24 را پیدا کنند یا می توانند جذر 24 را به این صورت تخمین بزنند: 01/24=9/4×9/4 که تقریباً با 24 برابر است.
توجه آن ها را به این حقیقت جلب کنید که این نمودار دیگر یک سهمی نیست ( نام این شکل هذلولی است ). از دانش آموزان بخواهید تا از روی نمودار اطلاعاتی به دست آورند: اگر محیط 30 واحد باشد، ابعاد مستطیل چه خواهد بود؟ اگر طول 7 واحد باشد، محیط آن چقدر است؟ اگر طول 24 واحد باشد، محیط چقدر است؟ برای دانش آموزان پایه ها بالاتر، این روند را می توان این گونه تعمیم داد:
(Aمعرف مساحت، P محیط، L طول و W عرض مستطیل است.) 4- زوج عامل هاهمه ی زوج هایی از عامل های عدد 36 را که ضربشان برابر 36 می شود، پیدا کنید. از دانش آموزان بخواهید تا همه مستطیل هایی را که مساحت آن ها 36 است مشخص کنند. اجازه دهید تا برای این کار از کاشی های مقوایی یا کاغذ شطرنجی استفاده کنند. برخی از دانش آموزان کشف خواهند کرد که این کار معادل با پیدا کردن زوج عامل های عدد 36 است. برای پیدا کردن مستطیلی که کوچکترین مساحت را دارد، لازم است تا دانش آموزان مستطیلی را پیدا کنند که از همه به مربع شبیه تر باشد. یا زوج عاملی را بیابند که پس از آن عامل ها دیگر تکرار می شوند. برای 36 زوج عامل های زیر را داریم: 1×36 2×18 3×12 4×9 6×6 9×4 12×3 18×2 36×1زوج های عامل های 36، بعد از زوج (6،6) تکرار می شود و از آن جا که هر دو عامل این زوج با هم برابرند، بنابراین یک مربع خواهیم داشت. به دانش آموزان فرصت دهید تا مساحت های 12، 28 یا 64 را هم تجربه و آزمایش کنند. از آن ها بخواهید تا حدس بزنند که در کجا عامل ها شروع به تکرار شدن خواهند کرد. از آن ها بپرسید که اگر قرار باشد همه ی زوج عامل های مربوط به یک عدد را پیدا کنند، چه تعداد عدد را باید آزمایش کنند؟ ( یک عدد که در صورت مجذور شدن نزدیکترین عدد به عدد اصلی باشد، برای 12 عدد 3، برای 28 عدد 5، برای 64 عدد 8، ..... )از دانش آموزان بپرسید که آیا می توانند پیش بینی کنند که کدام عددها مربع کامل هستند؟ ( مربع یک عدد صحیح ) عددی مربع کامل است که زوج عاملی با دو عدد یکسان داشته باشد، یا تعداد عامل های آن فرد باشد. 5- محیط ثابت برای شکل های مسطح ( دو بعدی )برای یک محیط ثابت، کدام شکل های دو بعدی بزرگترین مساحت را دارند؟ اگر ما تحقیق و بررسی خود را گسترش دهیم و سایر شکل های دو بعدی را هم، مانند چند ضلعی ها و دایره ها در نظر بگیریم، دانش آموزان می توانند کشف کنند که دایره شکلی است که از بین شکل های دو بعدی با محیط ثابت، بزرگترین مساحت را دارد. به دانش آموزان یک رشته نخ 20 سانتی متری و یک برگ کاغذ شطرنجی بدهید.مترجم: یوشا حکمی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 1155]
-
گوناگون
پربازدیدترینها