محبوبترینها
چگونه با ثبت آگهی رایگان در سایت های نیازمندیها، کسب و کارتان را به دیگران معرفی کنید؟
بهترین لوله برای لوله کشی آب ساختمان
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1844894573
دسته های مربع
واضح آرشیو وب فارسی:تبیان: دسته های مربع
اهدافدانش آموزان:- راه های یافتن معادلات شامل ریشه های مجذور و مکعبات را تحقیق خواهند کرد.- در مورد ارتباط بین بیان هندسی و عددی مجذور ها و ارتباط بین اعداد مربع کامل و جذر آن ها پیش بینی هایی می کنند.در مورد دلایلشان بحث و گفتگو خواهند کرد. وسایل لازم- برگه ی فعالیت بازی با مربع ها - پوستر، ماژیک، خط کش- کاغذ شطرنجی طرح درسدانش آموزان، درس را با تحقیق روی رادیکال ها آغاز می کنند. قبل از این که دانش آموزان الگوریتم های سنتی جمع رادیکال ها را ببینند، باید به آن ها فرصت داده شود تا مفهوم ریشه ی دوم یا جذر را کاوش کنند. این درس به آن ها این فرصت را می دهد. بعد از این که تحقیقاتشان را انجام دادند، شما می توانید به آن ها کمک کنید تا ارتباط بین روش های متنوعشان و ارتباط بین این روش ها و الگوریتم های سنتی را مشاهده کنند. برای شروع، ساختار این درس را برای دانش آموزان مرور کنید: 1- تحقیق و برسی در گروه ها 2- جمع آوری ایده ها به صورت یک پوستر3- ایجاد نمایشگاهی از پوستر ها 4- بحث کلاسی در مورد پوسترها همچنین، دانش آموزان را از وسایل و ابزاری که برای آن ها آماده می کنید، مطلع کنید (برگه ی پوستر، ماژیک، صفحه ی شطرنجی، قیچی و غیره.). توجه کنید که روی هر وسیله، بیش از حد تأکید نکنید، گرچه اگر شما استفاده از یک وسیله ی مشخص را پیشنهاد دهید، دانش آموزان آن را به عنوان تذکری در مورد چگونگی انجام تحقیق به کار خواهند برد. دانش آموزان را به گروه های 4 نفره تقسیم کنید و به هر گروه یک کپی از برگه ی فعالیت بازی با مربع ها را بدهید. توزیع فقط یک کپی از برگه ی فعالیت بین هر گروه، می تواند باعث تشویق دانش آموزان به بحث با یکدیگر شود. قبل از آغاز به کار، دانش آموزان را مطلع کنید که این کار، آسان نیست و آن ها نباید نگران شوند و دست از تلاش بردارند. آن ها را تشویق کنید که روی هر جنبه ای از فعالیت که برای آن ها جذاب تر یا قابل دسترس تر است، تمرکز کنند. به گروه ها در حدود 50 دقیقه وقت دهید تا پوستر را کامل کنند. شما در خلال این زمان چه کار باید بکنید؟ اگر شما تذکرات و نکته هایی را به دانش آموزان بگو یید، آن ها احتمالاً روش های متفاوتی برای کامل کردن این کار می یابند. شما باید دانش آموزان را از وقت مطلع کنید.
در ابتدای کلاس بعدی، از گروه ها بخواهید که پوستر هایشان را به دیوار آویزان کنند و کلاس را به بازدید از این نمایشگاه دعوت کنند. این درس را با هدایت کلاس به سمت گفتگویی در مورد کار دانش آموزان به پایان برسانید. سؤالاتی که می توان مطرح کرد: - بعد از دیدن پوستر گروه های دیگر، شما از دوستانتان چه سؤالاتی دارید؟- روش های مختلفی را که شما و دوستانتان برای یافتن دسته های معادل از مربع ها یافته اید، شناسایی و دسته بندی کنید. (توجه: این سؤال ساده ای نیست. شما از آن ها نمی خواهید که چیزها را شناسایی کنند، از آن ها خواسته می شود که چگونه شناسایی کردن را بیابند. آن ها باید به تفاوت ها و شباهت های بین برخورد گروه های مختلف با مسئله توجه کنند.) - برای هر روش داده شده، چه خصوصیاتی آن را از روش های دیگری که توسط گروه های دیگر استفاده شده است، مجزا می کند؟ - یک ویژگی را که بین همه ی روش ها رایج است، بیابید. [همه ی روش ها شامل مربع کامل می با شد.] - بعد از مشاهده ی کارهای دیگران، آیا شما می توانید به روش های دیگر حل مسئله فکر کنید؟ راه حل های ممکن برای برگه ی فعالیت بازی با مربع ها دسته ای از مربع ها با ارتفاع یکسان با مربعی به مساحت 72cm2:2-2-2-2-2-28-2-2-2-28-8-2-28-8-818-2-2-218-8-218-1832-2-232-850-2 - این لیست کاملی است، مگر این که ترتیب مربع ها مهم باشد. توجه کنید که از دانش آموزان نخواهید که لیست کاملی بدهند، از آن ها فقط بخواهید تا تعدادی از آن ها را بیابند. مربع ها که تقسیماتی با ارتفاع مساوی ندارند: اگر مساحت مربع به یک مربع کامل (4، 9، 16 و ...) بخش پذیر نباشد، آن گاه آن نمی تواند به مربع هایی که دارای مساحت هایی با اعداد طبیعی هستند، تقسیم شود. - چگونگی یافتن دسته هایی که ارتفاع آن ها با مربع داده شده، معادل باشند: یافتن این روش، قلب مسئله است. حداقل چندین راه برای انجام این کار وجود دارد. البته یک روش می تواند این باشد که ارتفاع مربع اصلی را بیابید، رابطه ای معادل با آن یافته و مربع هایی با این ارتفاع برای شکل دادن دسته ها بسازید. در مورد مثال برگه ی فعالیت، می توان این روش را به کار برد، چون:
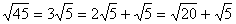
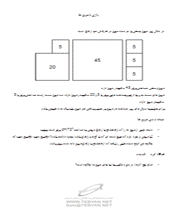
اما این روش نیازمند الگو ریتم هایی برای کار کردن با رادیکال ها می باشد. در این درس، فرض شده است که دانش آموزان این الگوریتم ها را می دانند. دانش آموزان باید راه هایی برای کار با این مسئله بیابند. زیبایی این تحقیق و بررسی در این است که روش هایی که دانش آموزانتان می یابند، به صورت جالبی با الگوریتم های سنتی که آن ها یاد خواهند گرفت، ارتباط پیدا می کند. برای مکعب ها به جای مربع ها:اگر ما به جای مجذور و جذر، از مکعب و ریشه ی سوم استفاده کنیم، می توانیم مکعب ها را تقسیم کنیم. برای مثال، مکعبی با حجم 54cm3 با مکعب هایی به حجم های 16cm3 و 2cm3 که روی هم دیگر قرار گرفته اند، هم ارتفاع است، زیرا: پرسش هایی برای دانش آموزان با استفاده از ریشه های دوم، برای نمایش ارتفاع های هر یک از مربع ها، معادله ای بسازید که نشان دهد ارتفاع های دو دسته با هم برابر است. (این سؤال باید با استفاده از دسته های مختلف تکرار شود.) [معادله به دسته ای که دانش آموزان استفاده می کنند، بستگی خواهد داشت. برای مثال، اگر دانش آموزان مشخص کنند که یک مربع به مساحت 45cm2، با دسته هایی که شامل مربع هایی به مساحت 20cm2 و 5cm2 می باشد، هم ارتفاع است، معادله ی زیر را می توان نوشت:
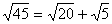
معادله های مشابهی را برای دسته های دیگر، می توان نوشت.] یک جفت از دسته هایی را که با هم تطبیق دارند و در هیچ یک از پوسترها نشان داده نشده اند، رسم کنید. در ذهن خود، تمرین کنید، سعی کنید شکلی بسازید که هیچ کس دیگری به آن فکر نکرده است. سپس، معادله ای بنو یسید که این هم ارزی را نشان دهد. [جواب ها متفاوت خواهد بود، اما اگر دانش آموزان به استفاده از اعداد بزرگ تشویق شده باشند، بهتر می توانند نتایج را تعمیم دهند.] روشی را برای نوشتن معادلات، بدون رسم مربع ها شرح دهید. اگر لازم بود، از مثالی خاص برای توضیح روشی که برای هر رادیکالی کار می کند، استفاده کنید. [تعیین کنید که آیا عدد زیر رادیکال، شامل فاکتوری که مربع کامل باشد، هست یا خیر. اگر بود، جذر آن عدد می تواند از زیر رادیکال بیرون بیاید و در کنار آن نوشته شود. سپس، عدد بیرون آمده از رادیکال را به مقدار های مختلف تجزیه می کنیم. برای مثال، عدد 18 شامل فاکتور 9، که یک مربع کامل است، می باشد. در نتیجه،
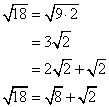
برای این مثال خاص، معادله های دیگری نیز وجود دارد. به هر حال مراحل یافتن هر معادله، یکسان است.] ارزشیابیاین تحقیق یک فرصت عالی برای ارزشیابی غیر رسمی، فراهم می کند. همین طور که شما راه می روید و به فعالیت دانش آموزان روی مسئله توجه می کنید، شما از روشی که دانش آموزان به ریاضیات فکر می کنند، مطلع می شوید. و برخی از چیزهای که شما می شنوید احتمالاً تعجب خواهید کرد، چگونه آن ها می توانند بعد از این همه سال ریاضیات، اینطور فکر کنند؟ دیگران وقتی روش هایی را که قابل پیش بینی نیست، کشف می کنند، شما را نسبت به بینشتان حیران می کند. اگر شما می خواهید که کار دانش آموزان را ارزیابی کنید، گزینه های مختلفی در دسترس می باشد. با توجه به این که شما چه چیزی را می خواهید ارزیابی کنید، ممکن است بخواهید مهارت حل مسئله، قدرت استدلال، کیفیت ارتباطات، دقت ریاضی یا سطح انجام کار را ارزیابی کنید. شما می توانید به پوسترها (و در نتیجه به نتایج گروهی) نمره دهید و یا می توانید به دانش آموزان با توجه به میزان شرکتشان در فعالیت نمره دهید. همچنین می توانید به دانش آموزان به طور فردی، با توجه به ارائه ی گزارش کارشان با استفاده از تفکر و تعمیم، نمره دهید. برای دانش آموزان مهم است که بفهمند چگونه ارزیابی می شوند. توسعه1- از دانش آموزان بخواهید به تعمیم این تمرین در فضای سه بعدی، از جنبه ی دیگری نگاه کنند. به آن ها بگویید وقتی مربع ها را تقسیم می کنید، شما اشیای (مربع های) دو بعدی را در یک بعد (ارتفاع ) مقایسه می کنید. در مورد مقایسه ی اشیای سه بعدی (مکعب)، در دو بعد (مساحت)، چه می توان گفت؟ روشی برای پوشاندن وجه یک مکعب بزرگ تر، با استفاده از مکعب های کوچک تر، بیابید. برای مثال، شکل مقابل، شش مکعب کوچک تر را که دقیقاً وجه یک مکعب 54cm3 را پوشانده اند، نشان می دهد. حجم هر یک از مکعب های کوچک چقدر است؟ روشی برای یافتن چینش دیگری از مکعب ها با وجه های منطبق، توصیف کنید. (مانند دسته ی مربع ها، فقط از اعداد طبیعی استفاده کنید.) 2- برای دانش آموزان کپی هایی از روش های متفاوتی که به آن ها دقت نکرده اند، تهیه کنید. از آن ها بخواهید تا توضیح دهند که چگونه این روش ها با روش هایی که آن ها مطرح کرده اند، مرتبط می شود. 3- اعداد را روی تکه های کاغذ بنویسید (و برای محرمانه بودن تا بزنید) و در جعبه ای بریزید. از هر یک از دانش آموزان بخواهید که یک عدد از داخل جعبه بیرون آورند. وقتی شما گفتید حرکت، آن ها اعدادشان را باز می کنند و دانش آموزانی را می یابند که با اعداد آن ها بتوانند یک معادله بسازند. برای مثال، دانش آموزانی با اعداد 5، 20 و 45 می توانند با ساختن یک معادله، یک گروه تشکیل دهند. نقشه ی کار این طور است که هر فردی باید در گروهی باشد و هر نفر، عدد دیگران را فقط یک بار می تواند به کار ببرد. ابتدا شما باید مجموعه اعدادی را که می توان به کار برد، آماده کنید. به عنوان مثال، اگر کلاس شما 25 دانش آموز دارد، می توانید از این مجموعه اعداد استفاده کنید: 3, 5, 5, 6, 12, 12, 12, 12, 20, 20, 24, 27, 27, 45, 45, 45, 48, 54, 54, 75, 80, 96, 108, 125, 150.این معما، احتمالات تعمیم یافته ی بی شماری دارد. شما می توانید از دانش آموزان بپرسید که چه تعداد پاسخ متفاوت وجود دارد. بررسی اجرای طرح درس در کلاس - دانش آموزان چگونه در این تحقیق و بررسی، شرکت کردند؟ چگونه می توان کلاس را به طور متفاوتی سازماندهی کرد (برای مثال، دانش آموزان را به روش دیگری گروه بندی کرد) تا مشارکت دانش آموزان در این فعالیت ها افزایش یابد؟ - چه قسمت هایی از این درس، به طور خاص برای دانش آموزان با هوش تر مفید است و کدام قسمت، برای دانش آموزانی که تلاش زیادی می کنند، مناسب است؟ چگونه می توانم دفعه ی بعد که از این درس استفاده می کنم، احتیاجات چنین دانش آموزانی را در نظر بگیرم؟- کیفیت پوسترهای دانش آموزان در قیاس با کیفیت بحث های ریاضیشان چگونه است؟ من چگونه می توانم به دانش آموزانم کمک کنم تا در بیان ریاضیاتشان در قالب نوشته، پیشرفت کنند؟ - در خلال این درس، چه مفاهیمی می توانند به کار دانش آموزان در پوسترهایشان مرتبط شوند؟ (لیستی از این رابطه ها تهیه کنید تا بتوانید در فرصت مناسب آن ها را برای دانش آموزانتان توضیح دهید.) مترجم: وحید رستمی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 4094]
-
گوناگون
پربازدیدترینها