محبوبترینها
دانلود آهنگ های برتر ایرانی و خارجی 2024
ماندگاری بیشتر محصولات باغ شما با این روش ساده!
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
بارش‌های سیل‌آسا در راه است! آیا خانه شما آماده است؟
قیمت انواع دستگاه تصفیه آب خانگی در ایران
نمایش جنگ دینامیت شو در تهران [از بیوگرافی میلاد صالح پور تا خرید بلیط]
9 روش جرم گیری ماشین لباسشویی سامسونگ برای از بین بردن بوی بد
ساندویچ پانل: بهترین گزینه برای ساخت و ساز سریع
خرید بیمه، استعلام و مقایسه انواع بیمه درمان ✅?
پروازهای مشهد به دبی چه زمانی ارزان می‌شوند؟
تجربه غذاهای فرانسوی در قلب پاریس بهترین رستوران‌ها و کافه‌ها
صفحه اول
آرشیو مطالب
ورود/عضویت
هواشناسی
قیمت طلا سکه و ارز
قیمت خودرو
مطالب در سایت شما
تبادل لینک
ارتباط با ما
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
مطالب سایت سرگرمی سبک زندگی سینما و تلویزیون فرهنگ و هنر پزشکی و سلامت اجتماع و خانواده تصویری دین و اندیشه ورزش اقتصادی سیاسی حوادث علم و فناوری سایتهای دانلود گوناگون
آمار وبسایت
تعداد کل بازدیدها :
1840383676
باقی ماندن یا عوض کردن؟
واضح آرشیو وب فارسی:تبیان: باقی ماندن یا عوض کردن؟ اهدافدانش آموزان قادرخواهند بود که : - از تناسب و مفاهیم پایه ای احتمال برای ساختن و امتحان کردن درس هایی در مورد نتیجه ی آزمایش ها و مدل سازی ها استفاده کنند. - احتمالات را برای پیش آمدهای حرکت ساده، با استفاده از روش هایی مانند نمودار درختی ( مدل های فضا یی ) محاسبه کنند. - راه کارهای متنوع مناسب برای حل مسئله ها به کار ببرند. وسایل لازم- یک صفحه چرخان با 3 ناحیه مساوی طرح درسشرح موقعیتدر طول مسابقه، به شرکت کننده ها سه در بسته نشان داده می شود. پشت یکی از درها جایزه ی بزرگی وجود دارد و پشت دو در دیگر اشیاء کم ارزشی وجود دارد. شرکت کننده ها یکی از درهای بسته را انتخاب می کنند. سپس میزبان بازی، یکی از درهای بسته که انتخاب نشده را باز می کند و شیء پشت در را آشکار می کند. در این جا به شرکت کننده این فرصت را می دهند که در صورت تمایل، انتخاب خود را تغییر دهد. در گروه ها، دانش آموزان می توانند با هم در مورد تصمیم گیری ها بحث کنند. مسئله اگر شما شرکت کننده باشید، کدام یک از راه کارهای زیر را انتخاب خواهید کرد، و چرا ؟ راه کار اول ( ادامه ی بازی با انتخاب اول ): در اول را عوض نکنید. راه کار دوم ( سکه انداختن ): یک سکه بیندازید، اگر رو آمد سر انتخاب اول خود باقی بمانید، و اگر پشت آمد انتخاب خود را عوض کنید . راه کار سوم ( تغییر دادن ): انتخاب خود را تغییر دهید . مردم چه می گویند: این بازی، چندین بار بین صدها نفر در کلاس ها و کارگاه های مختلف ارائه شده است و در موردش بحث شده است. در این جا برخی از واکنش های مردمی که برای اولین بار با این مسئله رو به رو شده اند، آورده شده است. چه فرقی می کند شما انتخابتان راعوض کنید یا همان را نگه دارید؟ شما برای بردن جایزه 50 درصد شانس دارید، چون تنها 2 در باقی می ماند. من روی انتخابم می مانم چون حس می کنم از ابتدا انتخاب درستی کردم. بعد از باز شدن یک در توسط میزبان، بازی بهتر می شود، چون فقط دو در باقی مانده است. در این موارد مهم نیست که شما سکه پرتاب کنید یا انتخابتان را تغییر دهید چون همه ی این احتمال ها یکسان است. من نمی فهمم که باز کردن یک در چگونه شانستان را افزایش می دهد: باز شدن یک در، فقط تردیدهایی به بازی اضافه می کند؟ در ابتدای بازی قبل از باز کردن درها، شانس شما برای برنده شدن یک به سه است، جالب این جاست که شانس شما حتی پس از باز شدن یکی از درها نیز یک به سه باقی خواهد ماند.چنین واکنش هایی درمیان مردم از هر صنفی و با هر دانش ریاضیاتی، از مبتدی تا معلم یا محققین ریاضی، اتفاق می افتد. یک رویکرد آموزشیدر تجربه، یک روش مناسب برای حل مسائل احتمالات، با حدس و آزمایش شروع شده و به مدل سازی کامپیوتری و تئوری منجر می شود. لذا توصیه می شود که دانش آموزان، ابتدا یک حدس در مورد بهترین راه کار ( باقی ماندن، سکه انداختن، تغییر دادن ) بزنند. در مرحله ی بعد آن ها می توانند با طرح یک آزمایش و مدل سازی کردن این وضعیت با سکه، طاس و یا اعداد رند، این بازی را تکرار کنند. بعد از آن می توان با استفاده از یک برنامه ی کامپیوتری، آزمایشی را که به صورت دستی انجام شده است، شبیه سازی کنند ( در این شبیه سازی می توان از اعداد بزرگ تر استفاده کرد. ). درنهایت، بسته به پیش زمینه ی دانش آموزان و سختی مسئله، ممکن است مدل سازی تئوری مسئله نیز مفید باشد. در این مسئله ی دشوار، مراحل مدل سازی قطعاً برای دانش آموزان دشوار خواهد بود تا بفهمند که درون هر یک از سه راه کار چه رخ می دهد. با استفاده از یک صفحه ی چرخان با مساحت های مساوی و یک سکه، ما می توانیم هر یک از سه راه کار را مدل سازی کنیم. برای تعیین این که کدام یک از سه راه کار بیشترین شانس برنده شدن را دارد، ما باید با هر یک از راه کارها چندین بار بازی کنیم و در هر بار نتایج به دست آمده را یادداشت کنیم. اجازه دهید تصور کنیم که جایزه پشت در A پنهان شده است، همان طور که در شکل 1 نشان داده شده است. به خاطر داشته باشید که میزبان باید دری را به ما نشان دهد که جایزه پشت آن نیست. اجازه دهید هر یک از راه کارها را بررسی کنیم.
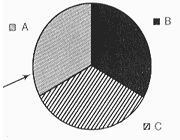
راه کار ادامه ی بازی با انتخاب اولالف- فرض کنید صفحه چرخان به در B می رسد، میزبان چه کاری انجام می دهد؟ ( به شما در B را نشان می دهد. ) شما چه می کنید؟ ( اگر در بازی باقی بمانید ) شما می برید یا می بازید؟ب- فرض کنید که صفحه ی چرخان به در C برسد. میزبان چه کاری انجام می دهد؟ ( به شما در B را نشان می دهد ) شما چه کار می کنید ( اگر باقی بمانید. ) آیا شما می برید یا می بازید؟ ج- فرض کنید که پس از انتخاب شما در صفحه ی چرخان به عنوان مثال میزبان می تواند به شما هر دو در B یا C را نشان دهد. شما چه کار می کنید ( اگر باقی بمانید ) آیا شما می برید یا می بازید؟ راه کار پرتاب کردن سکه: الف- فرض کنید که صفحه ی چرخان به در B می رسد و میزبان در C را باز می کند. شما یک سکه پرتاب می کنید تا تصمیم بگیرید که روی انتخاب اول( در B ) بمانید یا انتخابتان را به در A عوض کنید، شانس بردن جایزه برای شما چطور است؟ ب- فرض کنید که صفحه ی چرخان به در A برسد میزبان در B یا C را باز می کند. شما برای انتخاب کردن بین A و در دیگر سکه پرتاب می کنید. بار دیگر شانس شما برای بردن جایزه چقدر است؟ ج- فرض کنید که صفحه ی چرخان به در B برسد. میزبان در B یا C را باز می کند. شما برای انتخاب کردن بین A و در دیگر سکه پرتاب می کنید. این بار شانس شما برای بردن جایزه چقدر است؟ راه کار تغییر دادن : الف - فرض کنید که صفحه ی چرخان به در B برسد. میزبان در C را باز می کند. شما انتخابتان را عوض می کنید می برید یا می بازید؟ ب- فرض کنید که صفحه ی چرخان به در C برسد. میزبان در B را باز می کند. اگر شما در انتخابی خود را تغییر دهید، می برید یا می بازید؟ ج- فرض کنید که صفحه ی چرخان به در A برسد. میزبان در B یا C را به شما نشان می دهد. شما انتخاب خود را تغییر می دهید،به نظرتان می برید یا می بازید؟ ( توجه: اگر می خواهید که مسئله قدری راحت تر شود، راه کار پرتاب سکه را حذف کنید. ) ما توصیه می کنیم که به هر یک از دانش آموزان یک صفحه ی چرخان استفاده کند تا هر یک از سه راه کار را حداقل 100 بار امتحان کنند. این فعالیت تأثیر خوبی روی فهم دانش آموزان از مسئله دارد. پس از تکرار آزمایش های بسیار، می توان راه کار مناسبی را پیشنهاد کرد، تا با یک تئوری دقیق، احتمال بردتان را افزایش دهید. نتیجه 100000 بار بازی کردن معمای سخت میزبان با استفاده از کامپیوتر با هر یک راه کارها در جدول 1 آمده است. نتیجه پیامده چیست؟ بزرگترین سوال در مسئله میزبان 1- شما چه می دانید ؟ 2- شما چه وقت آن را می فهمید؟ است. باختن بردن راهکار 67405 32595 باقی ماندن 48837 51163 پرتاب کردن سکه 32597 67403 تغییر دادن در حل مسئله، به موارد سختی که می توانند اغلب بینش با ارزشی به ما بدهند، دقت کنید. فرض کنید میزبان امکان انتخاب یک در از 100 در را به ما می دهد که فقط پشت یکی از درها جایزه است.بعد از انتخاب شما، میزبان اعلام می کند که جایزه پشت در شما هست یا خیر؟ پس از اعلام، به شما فرصت داده می شود تا انتخابتان را تغیر دهید، چه کار می کنید؟ در این وضعیت، اکثر مردم علاقه دارند از راه کار عوض کردن استفاده کنند. دلایل آن ها ممکن است از این قبیل باشد: انتخاب اصلی این در 99 درصد احتمال باخت دارد. یعنی این که، در دیگر که میزبان نشان می دهد 99 درصد احتمال بردن دارد. یک مدل سازی کامپیوتری از این مسئله اصلاح شده این تحلیل را پشتیبانی می کند. به طور مشابه، در مثال 3 در، تا موقعی که احتمال این که انتخاب شما یک اشتباه با شد 3/2 (دو به سه) است،احتمال این که جایزه بعد از باز شدن یک در پوچ توسط میزبان، پشت دری باشد که شما انتخاب نکردا ید نیز 3/2 دو به سه است. با این حال، اکثر مردم کاملاً متقاعد شده اند که احتمال در انتها ½ است، حتی بعد از این که به آن ها پیشنهاد داده می شود که ا نتخابشان را تغییر دهند. اجازه دهید که ما تحلیل دقیق از مدل سازی صفحه گردان با استفاده از نمودار درختی، ارائه دهیم. یکبار دیگر، فرض کنید که جایزه پشت در A است. ما صفحه گردان را می چر خانیم تا انتخاب اول خود را مشخص کنیم . برای انتخاب هر در 3/1 یک به سه احتمال وجود دارد. میزبان باید یک خانه ی پوچ را آشکار کند. به طور اتفاقی ما در A را به عنوان انتخاب اول خود مشخص می کنیم، میزبان هر یک از در های B و C رامی تواند به ما نشان دهد. فرض می کنیم احتمال این که میزبان در B را به ما نشان 2/1 و احتمال این که در C را نشان دهد نیز 2/1 یک به دو است اگر ما B را انتخاب کنیم، میزبان باید در C را نشان دهد. اگر ما C را انتخاب کنیم، میزبان باید B را نشان دهد، بنابراین، در ابتدا، ما نمودار درختی شکل ½ را فراهم می کنیم.
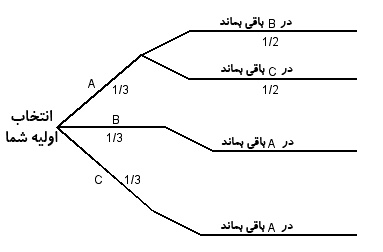
ما می توانیم این نمودار را به سه روش، مطابق با هر یک از راه کارهای باقی ماندن، پرتاب کردن سکه، یا عوض کردن، کامل کنیم. راه کارهای تغییر دادن و باقی ماندن را مشخص می کند که کدام یک در نهایت در هر شاخه، انتخاب می شوند. نمودار پرتاب کردن سکه، احتیاج به اضافه کردن 2 شاخه اضافی در هر مسیر دارد. در هر کدام احتمال 2/1 یک به دو دارد که به ما می گوید انتخاب اول خود را نگه داریم یا آن را تغییر دهیم. این سه نمودار در شکل های 3 و 4و 5 با احتمال نهایی که برای هر شاخه با استفاده از قاعده معمولی ضرب به دست آمده، نشان داده شده اند. دوباره، بدون کم کردن از اصل کلی، ما فرض کردیم که جایزه پشت در A قرار دارد.
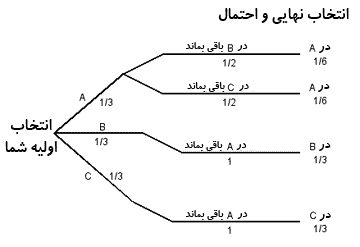
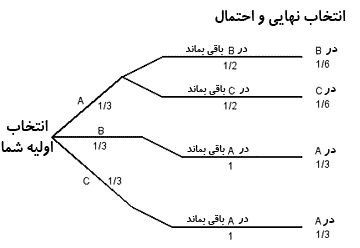
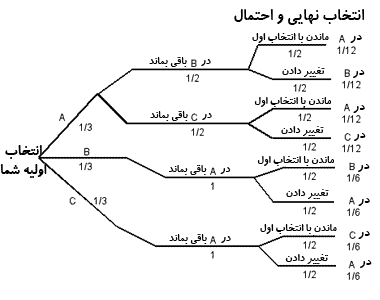
وقتی ما احتمال این که در نهایت کدام یک از در های A ، B یا C انتخاب می شود را فهرست می کنیم، پی می بریم که هر یک از راه کارها نتایج متفاوتی را عرضه می کند. احتمال این که در نهایت کدام در انتخاب شود در C در B در A راه کار 1/3 1/3 1/3 باقی ماندن 1/4 1/4 1/2 سکه انداختن 1/6 1/6 2/3 تغییر دادن در واقع، راهی را که اکثر مردم در ابتدا برای این مسئله انتخاب می کنند، شگفت انگیز نمی باشد. تصور اشتباه از شانس در میان دانش آموزان ما و حتی کارشناسان رواج دارد، می توانید با مطالعه و بررسی این مثال، حدس های احتمال در انتخاب درها اصلاح کنید. مو قعیت جدیدی را لحاظ کنید؛ شما در مسابقه اسب دوانی شرط بندی کرده اید و متعاقباً خبری دریافت کرده اید که بعد از بیرون کشیدن 6 عدد از میان یک میلیون عدد، عدد شما بین این 6 عدد قرار دارد و برنده از بین این 6 عدد انتخاب می شود. احتمال این که شما برنده شوید، چقدر است؟ اکثر مردم به طور عملی این تجربه را دارند و فکر می کنند که احتمال بردنشان یک در میلیون است به هر حال، اگر یک قرعه کشی جدید در میان این 6 عدد شود، در این وضعیت موقعیت کاملاً متفاوت است. شانس شما برای بردن به طور زیادی افزایش می یابد. فرض کنید، مطابق وضعیت دوم، شرط بندی انجام شود، احتمال شما برای بردن چگونه است؟ اگر بحث این مقاله معقول به نظر رسیده باشد، آیا شما برای انتخاب عددتان تاس پرتاب، نخواهید کرد! مترجم: وحید رستمیتنظیم: نسرین صادقی
این صفحه را در گوگل محبوب کنید
[ارسال شده از: تبیان]
[مشاهده در: www.tebyan.net]
[تعداد بازديد از اين مطلب: 634]
-
گوناگون
پربازدیدترینها