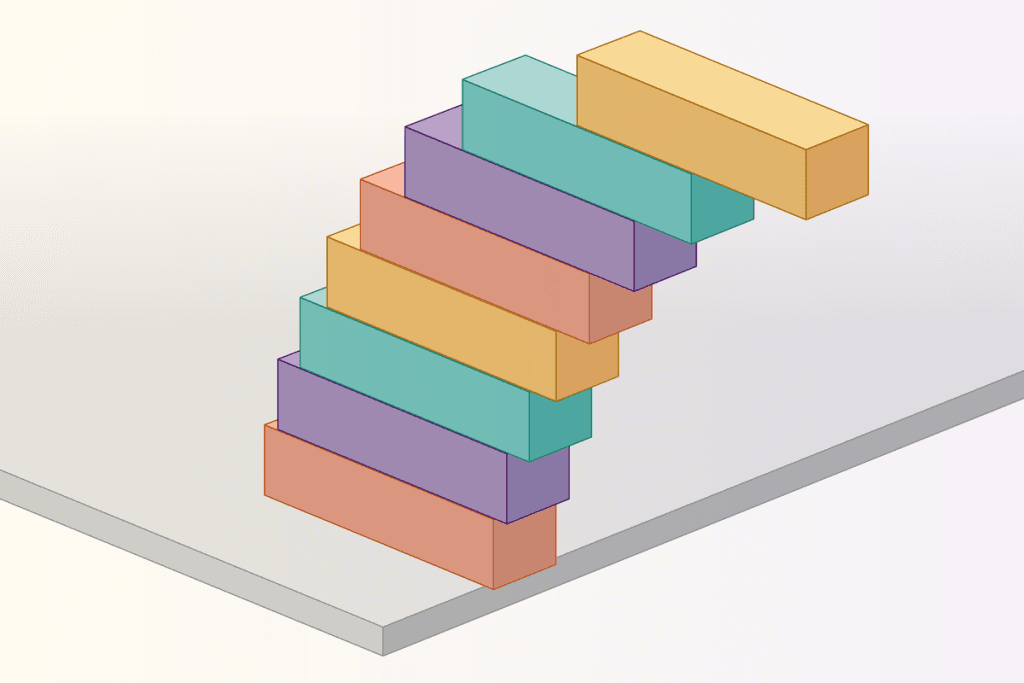
معمای غیرممکن چیدن بلوکها: راهحلی باورنکردنی که میتوانید در خانه آزمایش کنید!
پل بیپایان بلوکها: از گرند کانیون تا بینهایت!
نوشته: جک مورتاگ
ویرایش شده توسط جینا براینر
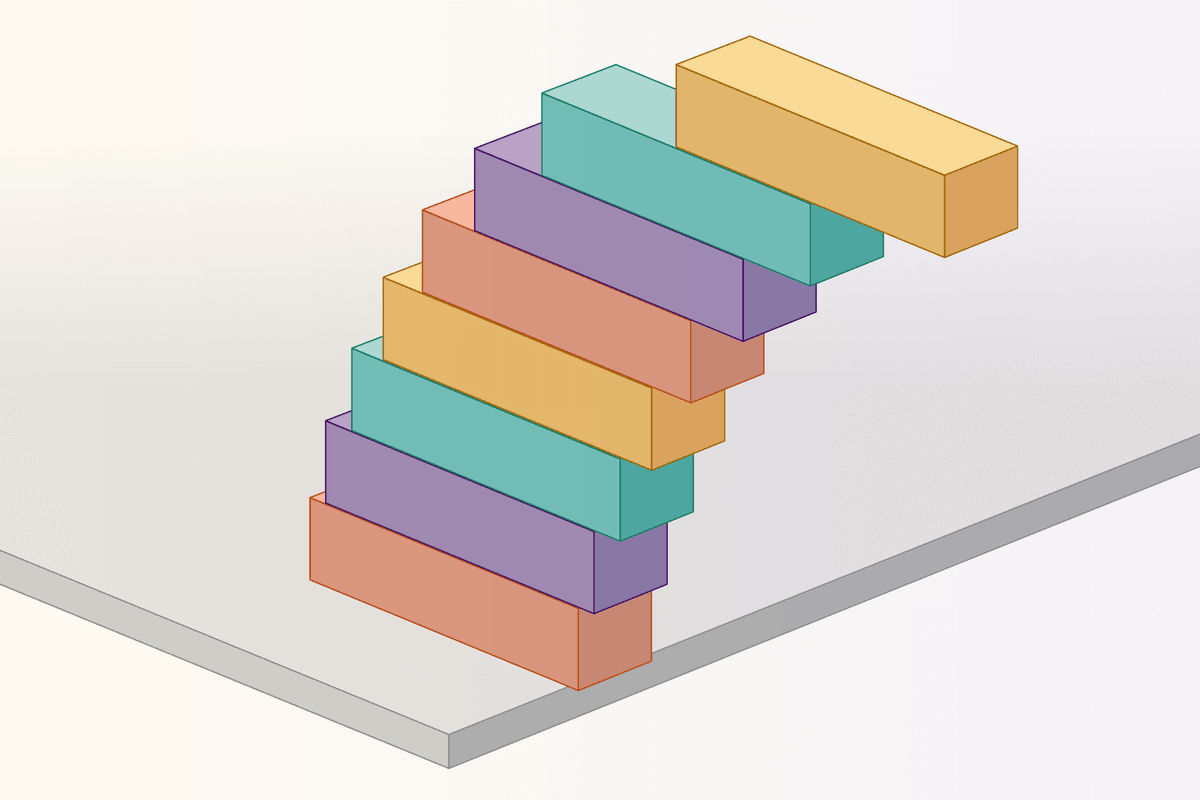
آیا میدانستید با چیدن بلوکها میتوان پلی ساخت که بدون نیاز به چسب، تا بینهایت ادامه یابد؟ این آزمایش ساده ریاضی را میتوانید در خانه امتحان کنید:
آزمایشی شگفتانگیز با بلوکهای کودکانه
۱. یک بلوک را روی میز قرار دهید و آرام آن را به سمت لبه میز فشار دهید تا نیمی از آن بیرون بزند.
۲. حال دو بلوک را روی هم بچینید. حداکثر بیرونزدگی ممکن چقدر است؟
۳. این کار را با بلوکهای بیشتر ادامه دهید. آیا میتوان کل طول یک بلوک را از لبه میز بیرون زد؟ دو برابر طول بلوک چطور؟
پاسخ شگفتانگیز است: این پل بلوکی میتواند تا بینهایت ادامه یابد! در تئوری، میتوان با بلوکهای آزاد، پلی روی گرند کانیون ساخت – بدون نیاز به چسب!
محدودیتهای دنیای واقعی
البته در عمل، عواملی مانند ناهمگونی بلوکها، جریان هوا و وزن سازه، این آرزو را محدود میکنند. اما در دنیای ایدهآل ریاضی، این امکان وجود دارد. کلید این معما در دو مفهوم نهفته است:
۱. مرکز جرم: نقطهای که میتوان تمام وزن جسم را در آن متمرکز تصور کرد.
۲. سری هارمونیک: یکی از مشهورترین سریهای نامتناهی در ریاضیات.
مرکز جرم و تعادل
برای یک بلوک یکنواخت، مرکز جرم دقیقاً در وسط آن قرار دارد. تا زمانی که مرکز جرم بالای سطح میز باشد، بلوک نمیافتد. این توضیح میدهد که چرا یک بلوک تنها میتواند تا نیمی از طولش بیرون بزند.
محاسبات دو بلوکی
فرض کنید هر بلوک طول و جرمی برابر ۱ دارد:
- بلوک بالایی میتواند ۱/۲ واحد از بلوک زیرین بیرون بزند.
- بلوک پایینی فقط میتواند ۱/۴ واحد از لبه میز بیرون بزند.
در این حالت، مرکز جرم ترکیبی دقیقاً بالای لبه میز قرار میگیرد.
الگوی کلی
با افزایش بلوکها، این الگو ادامه مییابد:
- بلوک اول: ۱/۲
- بلوک دوم: ۱/۴
- بلوک سوم: ۱/۶
- بلوک چهارم: ۱/۸
- و به همین ترتیب…
ارتباط با سری هارمونیک
اگر این مقادیر را جمع بزنیم، به سری زیر میرسیم:
۱/۲ + ۱/۴ + ۱/۶ + ۱/۸ + ۱/۱۰ + …
این دقیقاً نصف سری هارمونیک معروف است:
۱ + ۱/۲ + ۱/۳ + ۱/۴ + ۱/۵ + …
که به آرامی ولی تا بینهایت رشد میکند.
آزمایش عملی
با چهار بلوک میتوانید کل طول یک بلوک را از لبه میز بیرون بزنید:
۱/۲ + ۱/۴ + ۱/۶ + ۱/۸ ≈ ۱.۰۴۲
نویسنده این مقاله با استفاده از کارتهای بازی این آزمایش را انجام داده و موفق شده است یک کارت را کاملاً از لبه میز بیرون بزند!
حقایق جالب
- برای رسیدن به دو برابر طول بلوک، به ۳۱ بلوک نیاز دارید.
- حتی با ۱۰۰ میلیون بلوک، فقط به حدود ۹.۵ برابر طول بلوک میرسید.
- در مقیاسهای بزرگ، قوانین فیزیک مانع از تحقق این ایده میشوند.
اما در دنیای ایدهآل ریاضیات، هیچ حدی برای این بیرونزدگی وجود ندارد!