معمای چیدن بلوکها: راهحلی شگفتانگیز که فیزیک را متحول کرد!
نویسنده: جک مورتاگ
ویرایش شده توسط: جینا براینر
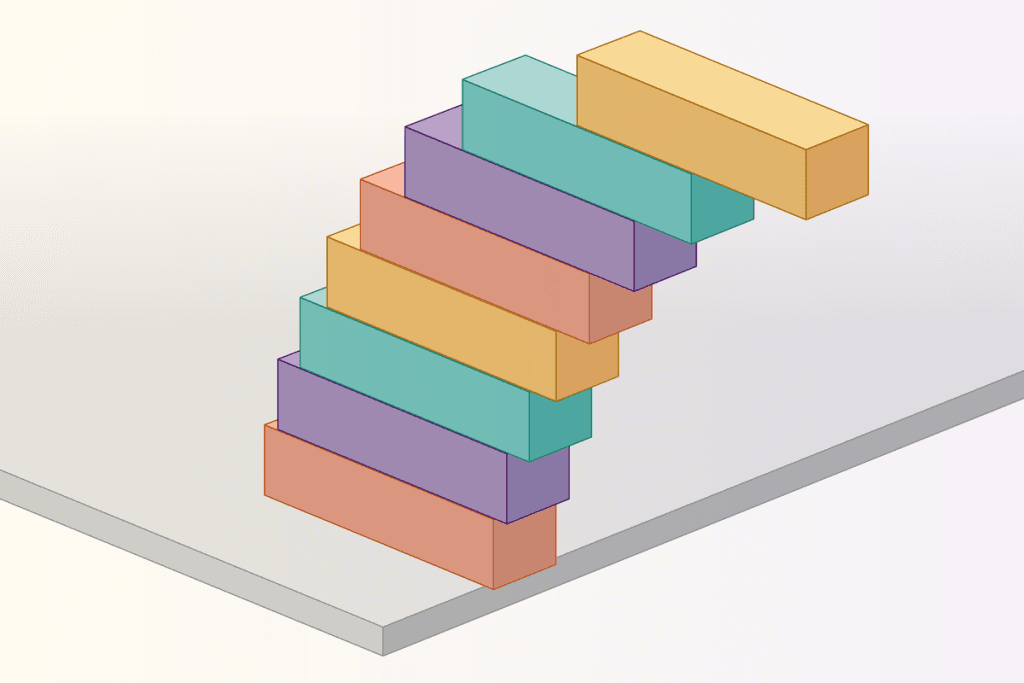
تصویر هشت بلوک رنگارنگ که به صورت پلکانی روی میز چیده شدهاند و هر کدام نسبت به لبه میز فاصله متفاوتی دارند
یک آزمایش ساده با نتایج حیرتانگیز
این آزمایش جالب را میتوانید در خانه امتحان کنید: چند بلوک اسباببازی بردارید و روی میز بچینید. یک بلوک را به آرامی به سمت لبه میز فشار دهید تا جایی که نیمی از آن از لبه میز آویزان شود. حالا دو بلوک را روی هم قرار دهید – حداکثر فاصلهای که میتوانید بلوک بالایی را از لبه میز بیرون ببرید چقدر است؟
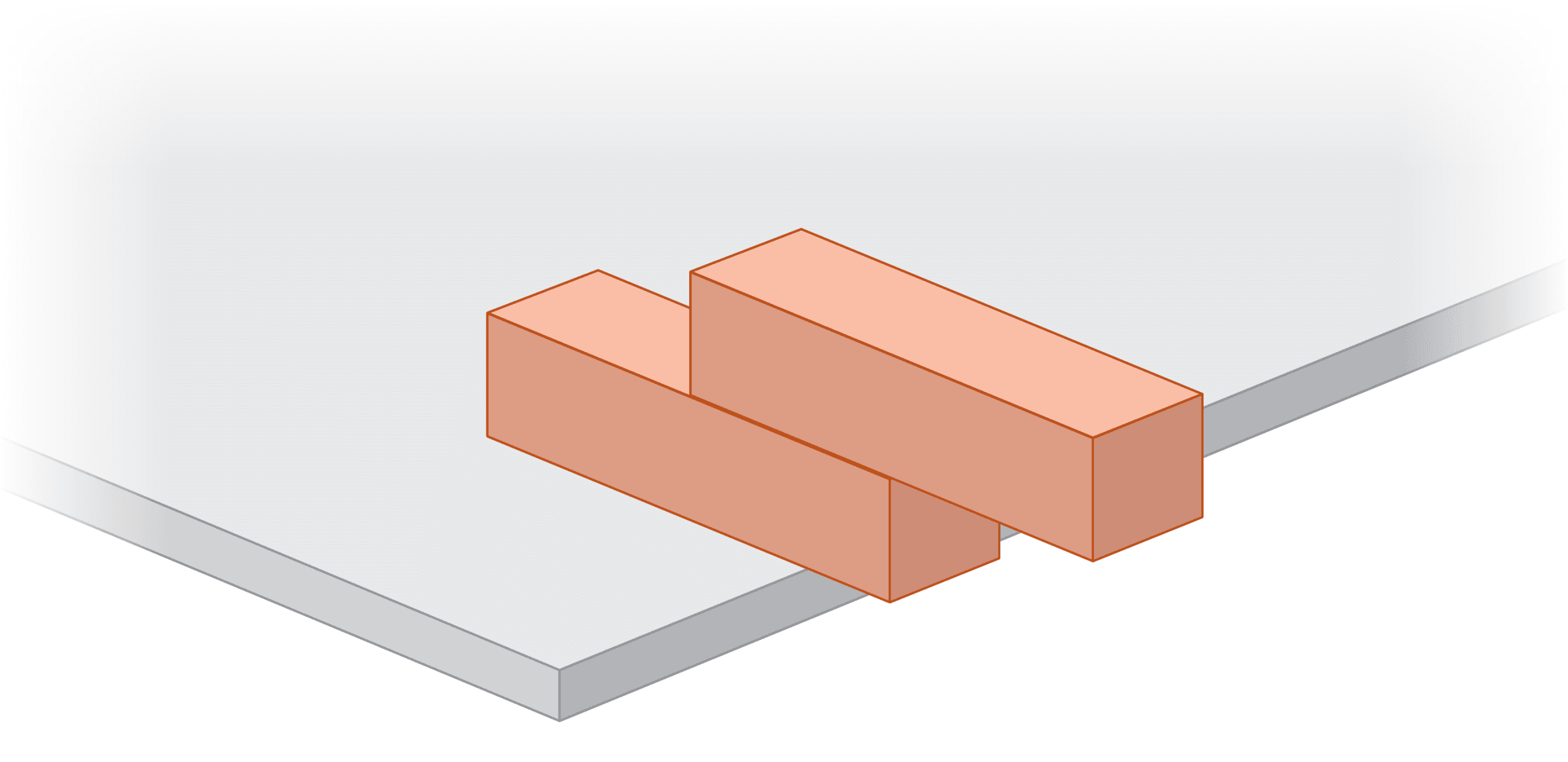
نمایش دو بلوک که بلوک پایینی کمی از لبه میز فاصله دارد و بلوک بالایی نصف طول خود را از بلوک پایینی بیرون زده است
معمایی با پاسخ نامحدود!
اگر این کار را با بلوکهای بیشتری ادامه دهید، حداکثر فاصلهای که میتوانید ایجاد کنید چقدر خواهد بود؟ آیا ممکن است کل طول یک بلوک از لبه میز فاصله بگیرد؟ شاید دو برابر طول بلوک؟ پاسخ شگفتانگیز این است که این ساختار میتواند تا بینهایت ادامه یابد! در تئوری، میتوان پلی از بلوکهای روی هم چیده شده ساخت که حتی عرض گرند کنیون را هم پوشش دهد – بدون نیاز به چسب!
چالشهای دنیای واقعی
البته در عمل عواملی مانند ناهمگونی بلوکها، جریان هوا و وزن زیاد سازههای عظیم ممکن است این ایده را محدود کند. اما درک دلیل نامحدود بودن این امکان در دنیای ریاضیات، بینش جالبی ارائه میدهد. پاسخ این معما به دو مفهوم کلیدی وابسته است: سری هارمونیک در ریاضیات و مرکز جرم در فیزیک.
مرکز جرم و تعادل
وقتی یک بلوک را روی میز قرار میدهید، میتوانید نیمی از آن را از لبه میز بیرون ببرید بدون اینکه بیفتد. دلیل این امر مرکز جرم است – نقطهای که میتوان تمام وزن جسم را در آن متمرکز تصور کرد. تا زمانی که مرکز جرم بالای سطح میز قرار دارد، جسم پایدار میماند.
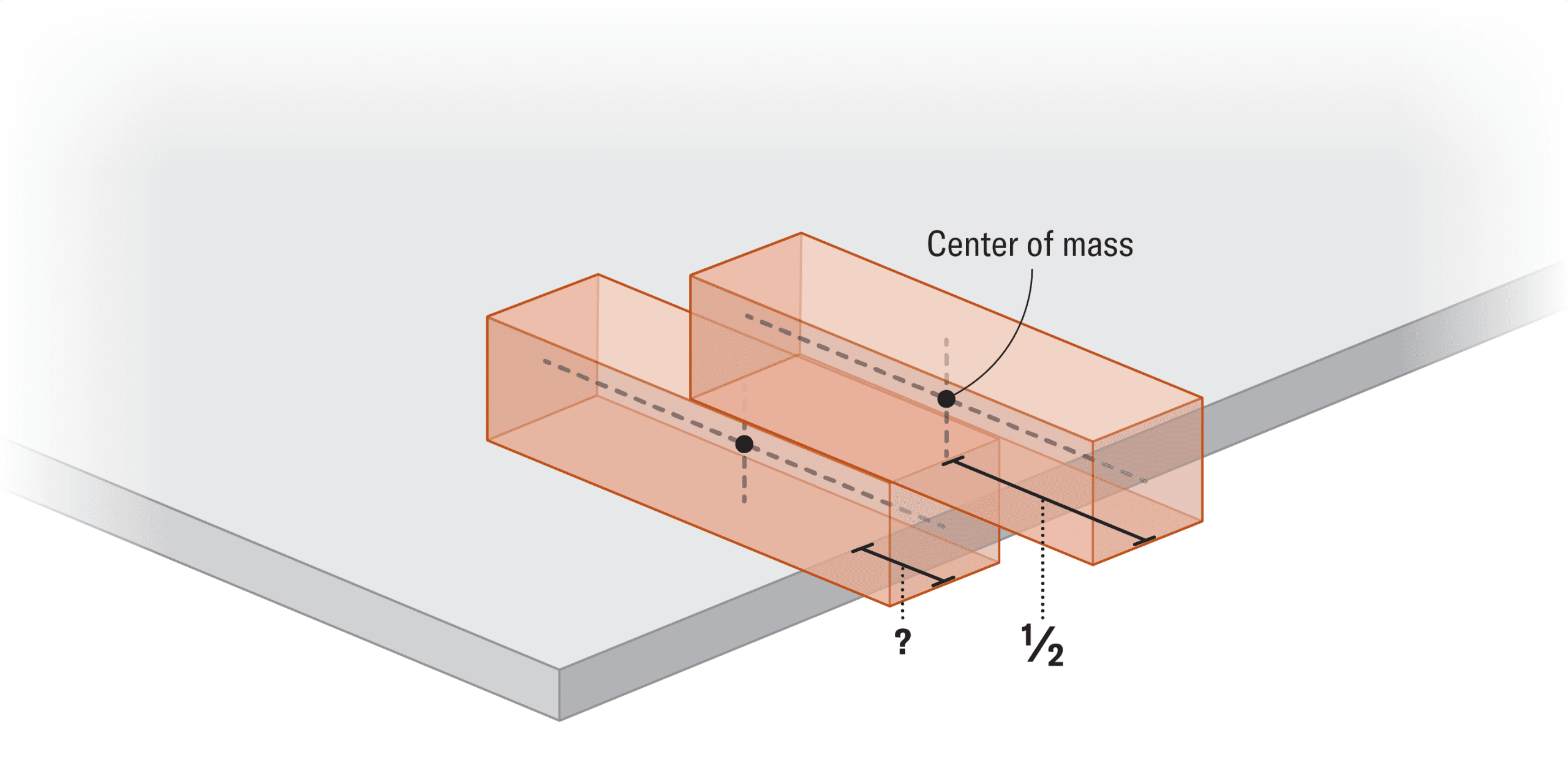
نمایش مرکز جرم دو بلوک شفاف که بلوک بالایی نصف طول خود را از بلوک پایینی بیرون زده است
الگوی ریاضی پشت معما
با اضافه کردن بلوکهای بیشتر، الگوی جالبی ظاهر میشود:
- بلوک اول: ۱/۲ طول از لبه بیرون میزند
- بلوک دوم: ۱/۴ طول
- بلوک سوم: ۱/۶ طول
- بلوک چهارم: ۱/۸ طول
- و به همین ترتیب…
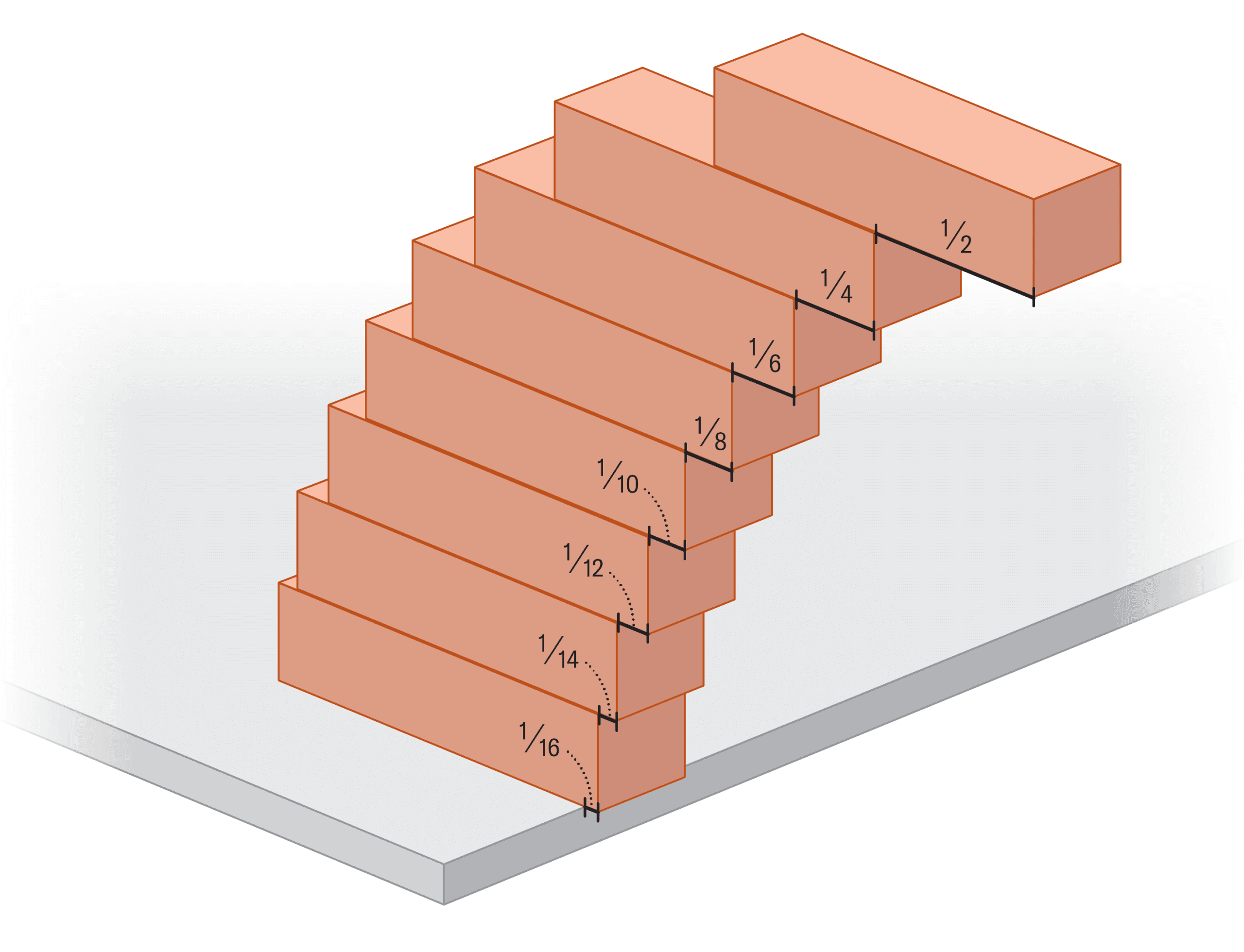
نمایش هشت بلوک با فاصلههای کسری مختلف از لبه میز
ارتباط با سری هارمونیک
اگر این کسرها را جمع بزنید، به الگویی شبیه سری هارمونیک میرسید – یکی از معروفترین سریهای نامتناهی در ریاضیات. جالب اینجاست که این سری اگرچه بسیار آهسته رشد میکند، اما در نهایت به بینهایت میل میکند. به همین دلیل است که در تئوری، میتوان سازهای با فاصله نامحدود از لبه میز ساخت!
آزمایش عملی
با چهار بلوک میتوانید بلوک بالایی را کاملاً از لبه میز بیرون ببرید (۱/۲ + ۱/۴ + ۱/۶ + ۱/۸ ≈ ۱.۰۴۲). من این آزمایش را با کارتهای بازی روی میز قهوهخوری امتحان کردم و پس از چند دقیقه تنظیم دقیق، موفق شدم کارت بالایی را کاملاً از لبه میز آویزان کنم – حسی مانند یک شعبدهباز واقعی داشتم!
محدودیتهای عملی
برای ایجاد فاصلهای به اندازه دو برابر طول بلوک، به ۳۱ بلوک نیاز دارید. جالب اینجاست که حتی با ۱۰۰ میلیون بلوک، فاصله ایجاد شده تنها حدود ۹.۵ برابر طول یک بلوک خواهد بود. پس برای پل زدن روی گرند کنیون به صبر و حوصله زیادی نیاز دارید! در ابعاد بسیار بزرگ، قوانین فیزیک مانع از تحقق این ایده میشوند، اما در شرایط ایدهآل ریاضی، این امکان واقعاً نامحدود است.